Datasheet

44
PRIM
TORTURE
WORKING
WITH
TINY
PRIMS
BUILDING
BY
THE
NUMBERS
TUTORIAL:
BUILDING A
STAIRCASE
CHAPTER 3
PRIM TORTURE
Prim torture is the phrase Second Life builders use to describe the sick, sadistic process of
morphing prims into exotic new shapes that even Linden Lab may not have anticipated. The results
can be useful, bizarre, artistic, and sometimes utterly paradoxical. This section will expand your
understanding of how prims really work and arm you with some tips and tricks to get the most bang
from your prim buck.
■ PATH CUT
A path cut causes a wedge gap to
appear in the prim such that the point of
the wedge lines up with the prim’s z-axis.
An easy way to visualize this is to imagine
the prim as a pie viewed from above, and
the path cut as a slice taken away by a
hungry kid. The cut will normally begin
in the corner of the prim for those that
have corners, such as boxes and prisms.
You can choose any value between 0 and
1 but there are eight commonly used
cuts you should commit to memory for
frequent use (Figure 3.1). Cut values
of 0.0, 0.25, 0.5, and 0.75 are used
to create diagonal cuts from corner to
corner while values of 0.125, 0.375,
0.625, and 0.875 create cuts from
edge to edge.
Path cuts are essential for creating
shapes that are more complex and
detailed than the basic building blocks
themselves. For example, to create a
drawer handle you could use a hollow
cylinder or torus and then cut it in half
(cut value 0.5). However, path cuts
can also be used to conserve prims.
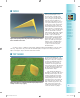
Let’s say you’re building a set of stairs,
each step 0.25 meters tall. You might
consider using one box for each step,
but by using cuts you can halve the
number of prims. Simply use a 0.5-
meter box path cuts of 0.125 and
0.875, creating an L-shaped prim.
Stacking these boxes corner to corner
would give you the exact same steps but
would consume only half the number of
prims (Figure 3.2)!
Figure 3.1: Commonly used cut values on a box prim
.625
.125
.750
.000
.875
.500
.250
.375
Figure 3.2: Four steps created using four prims (left),
and the same number of steps created using just two
prims (right)
042-057 Chapter 03.indd 44042-057 Chapter 03.indd 44 9/5/07 1:27:32 AM9/5/07 1:27:32 AM