User`s guide
124
Document 1: Bending Stress and Strain in Cantilever Beam
Recall, the definition of normal strain is
Using the line segments shown in Figure 1, the before and after length can be used to give
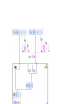
Figure 38 Bending of a Cantilever Beam
The line length on neutral axis remains same after bending. The length becomes shorter above
the neutral axis (for positive moment) and longer below. The line AB and A'B' can be described
using the radius of curvature, ρ, the differential angle, dθ, and the distance from A’B’ to the neutral
axis, y. The y coordinate is assumed upward from the neutral axis, where there is no strain.
Therefore we have
This relationship gives the bending strain at any location as a function of the beam curvature
and the distance from the neutral axis.
The strain equation above can be converted to stress by using Hooke's law, σ = Eε, giving,
Eq.1
Eq.2
Eq.3
Eq.4
Eq5