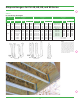
Technical Specifications
Series Depth
EI
2
(106 lbf-in�
2
)
Mr
3
(lbf-ft)
Vr
4
(lbf)
K
5
(106 lbf)
Self Weight
(plf)
Allowable Verticle
Load (lbf/ft)
PJI 40
9-1/2 193 2,735 1,120 4�94 2�6 2,000
11-7/8 330 3,545 1,420 6�18 2�9 2,000
14 482 4,270 1,710 7�28 3�1 2,000
16 657 4,950 1,970 8�32 3�4 2,000
PJI 60
9-1/2 231 3,780 1,120 4�94 2�6 2,000
11-7/8 396 4,900 1,420 6�18 2�9 2,000
14 584 5,895 1,710 7�28 3�1 2,000
16 799 6,835 1,970 8�32 3�4 2,000
PJI 80
11-7/8 547 6,940 1,420 6�18 3�6 2,000
14 802 8,360 1,710 7�28 3�8 2,000
16 1,092 9,690 1,970 8�32 4�0 2,000
18 1,413 11,000 2,450 9�36 4�3 2,000
20 1,790 12,180 2,530 10�4 4�5 1,720
22 2,214 13,340 2,615 11�44 4�7 1,440
24 2,687 14,490 2,695 12�48 4�9 1,390
PJI 90
11-7/8 601 8,515 1,420 6�18 3�6 2,000
14 877 10,255 1,710 7�28 3�8 2,000
16 1,187 11,895 1,970 8�32 4�0 2,000
18 1,546 13,445 2,450 9�36 4�3 2,000
20 1,957 14,885 2,530 10�4 4�5 1,720
22 2,419 16,305 2,615 11�44 4�7 1,440
24 2,934 17,710 2,695 12�48 4�9 1,390
P. 33
P3 Joist Design Properties
TABLE 19
P3 Joist Section Properties and Allowable Capacities
NOTES
1� The tabulated values are design values
for standard duration of load� All values,
except EI and K, shall be permitted to
be adjusted for other load durations as
permitted by the code�
2� Bending stiffness (EI) of the P3 Joist
3� Moment capacity of the P3 Joist which
shall not be increased by any code-
allowed repetitive member use factor�
4� Shear capacity (V) of the P3 Joist
5� Coefficient of shear deflection (K) of
the P3 Joist (For calculating uniform load
and center-point load deflections of the
P3 Joist in a simple-span application,
use Equations 1 and 2)�
1- Uniform Load:
δ = 5ω,
4
+ ω,
2
384EI K
2- Center-Point Load:
δ = P,3 + 2P,
48EI K
Where: δ = calculated deflection (in)
ω = uniform load (lbf/in)
, = design span (in)
P = concentrated load (lbf)
EI = bending stiffness of
the P3 Joist (lbf-in
2
)
K = coefficient of shear
deflection (lbf)