User manual

WaveSurfer 3000/3000z Oscilloscopes Operator's Manual

Choosing a Window

The choice of a spectral window is dictated by the signal's characteristics. Weighting functions control the

filter response shape, and affect noise bandwidth as well as side lobe levels. Ideally, the main lobe should

be as narrow and flat as possible to effectively discriminate all spectral components, while all side lobes

should be infinitely attenuated. The window type defines the bandwidth and shape of the equivalent filter

to be used in the FFT processing.

Rectangular windows provide the highest frequency resolution and are useful for estimating the type of

harmonics present in the signal. Because the rectangular window decays as a (sinx)/x function in the

spectral domain, slight attenuation will be induced. Functions with less attenuation (Flat Top and

Blackman-Harris) provide maximum amplitude at the expense of frequency resolution, whereas Hamming

and Von Hann are good for general purpose use with continuous waveforms.

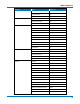
Window Type Applications and Limitations

Rectangular Normally used when the signal is transient (completely contained in the time-domain window)

or known to have a fundamental frequency component that is an integer multiple of the fun-

damental frequency of the window. Signals other than these types will show varying amounts of

spectral leakage and scallop loss, which can be corrected by selecting another type of window.

Hanning (Von Hann)

& Hamming

Reduces leakage and improves amplitude accuracy. However, frequency resolution is also

reduced.

Flat Top Provides excellent amplitude accuracy with moderate reduction of leakage, but with reduced

frequency resolution.

Blackman-Harris Reduces leakage to a minimum, but with reduced frequency resolution.

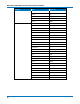
FFT Window Filter Parameters

Window Type

Highest Side Lobe

(dB)

Scallop Loss (dB)

ENBW

(bins)

Coherent Gain (dB)

Rectangular

-13 3.92 1.0 0.0

Von Hann

-32 1.42 1.5 -6.02

Hamming

-43 1.78 1.37 -5.35

Flat Top

-44 0.01 3.43 -11.05

Blackman-Harris

-67 1.13 1.71 -7.53