User guide
114 www.xilinx.com System Generator for DSP User Guide
UG640 (v 12.2) July 23, 2010
Chapter 1: Hardware Design Using System Generator
Browse Through and Understand the Xilinx Filter Block
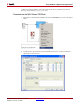
The following block diagram showing how the MAC-based FIR filter has been
implemented for this tutorial.
At this point, the MAC filter is set up for a 10-bit signed input data (Fix_10_8), a 12-bit
signed coefficient (Fix_12_12), and 43 taps. All these parameters can be modified directly
from the MAC block GUI. The coefficients and data need to be stored in a memory system.
For the tutorial, you choose to use a dual-port memory to store the data and coefficients,
with the data being captured and read out using a circular RAM buffer. The RAM is used
in a mixed-mode configuration: values are written and read from port A (RAM mode), and
the coefficients are only read from port B (ROM mode).
The multiplier is set up to use the embedded multiplier resource available in Xilinx
Virtex® devices as well as three levels of latency in order to achieve the fastest performance
possible. The precision required for the multiplier and the accumulator is a function of the
filter taps (coefficients) and the number of taps. Since these are fixed at design time, it is
possible to tailor the hardware resources to the filter specification. The accumulator need
only have sufficient precision to accumulate maximal input against the filter taps, which is
calculated as follows:
acc_nbits = ceil(log2(sum(abs(coef*2^coef_width_bp)))) + data_width+ 1;
Upon reset, the accumulator re-initializes to its current input value rather than zero, which
allows the MAC engine to stream data without stalling. A capture register is required for
streaming operation since the MAC engine reloads its accumulator with an incoming
sample after computing the last partial product for an output sample.
Finally, a downsampler reduces the capture register sample period to the output sample
period. The block is configured with latency to obtain the most efficient hardware
implementation. The downsampling rate is equal to the coefficient array length.