User`s guide

Creating LTI Models
2-17
it is often desirable to work with the descriptor form when the matrix is
poorly conditioned with respect to inversion.
The function
dss is the counterpart of ss for descriptor state-space models.
Specifically,
sys = dss(A,B,C,D,E)
creates a continuous-time DSS model with matrix dat a A,B,C,D,E.For
example, consider the dynamical mode l
withve ctor ofang ular velocities .I f theinertia matrix is poorlycond it ioned
with respect to inversion, you can specify this system as a descriptor model by
sys = dss(–F,eye(n),eye(n),0,J) % n = length of vector
Frequency Response Data (FRD) Models
Insomeinstances, you may only havesampled frequency responsedata,rather
than a transfer function or state-space model for the system you want to
analyze or control. For information on frequency response analysis of linear
systems, see Chapter 8 of [1].
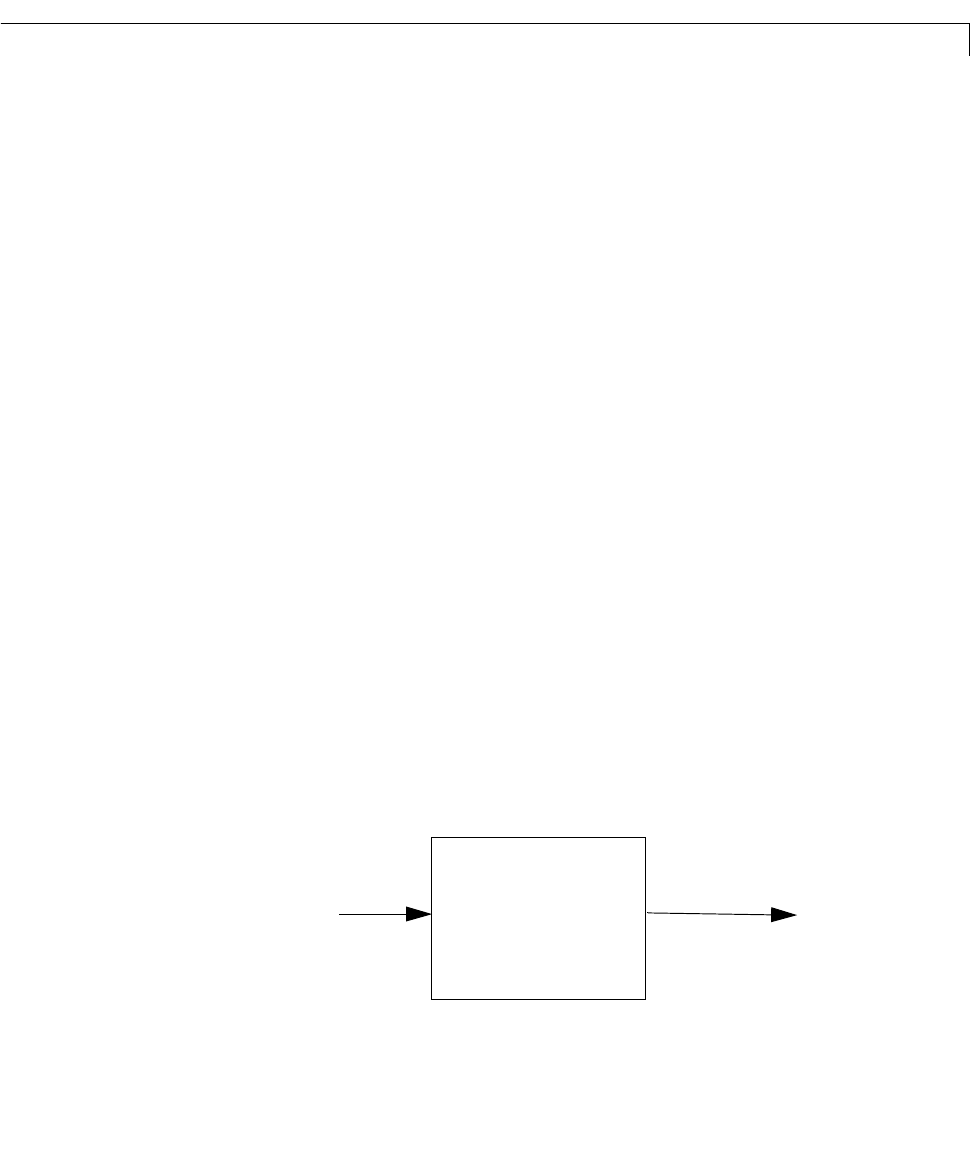
Forexample,supposethe frequencyresponsefunctionfor the SISOsystem you
want to model is G(w). Suppose, in addition, that you perform an experiment
to evaluate G(w) at a fixed set of frequencies, . You can do this by
driving the system with a sequence of sinusoids at each of these frequencies, as
depicted below.
E
J
dω
dt
--------
F ω+ T=
y ω=
ω
J
ω
w
1
w
2
…
w
n
,,,
w
i
tsin
G(w) =
y
i
t()