User`s guide

lqgreg
11-118
In discrete time, you can form the LQG regulator using either the prediction
of basedonmeasurementsupto , orthe currentstate
estimate based on all available measurements including . While
the regulator
is always well-defined, the current regulator
is causal only when is invertible (see
kalman for the notation). In
addition, practical implementations of the current regulator should allow for
the processing time required to compute once the measurements
become available (this amounts to a time delay in the feedback loop).
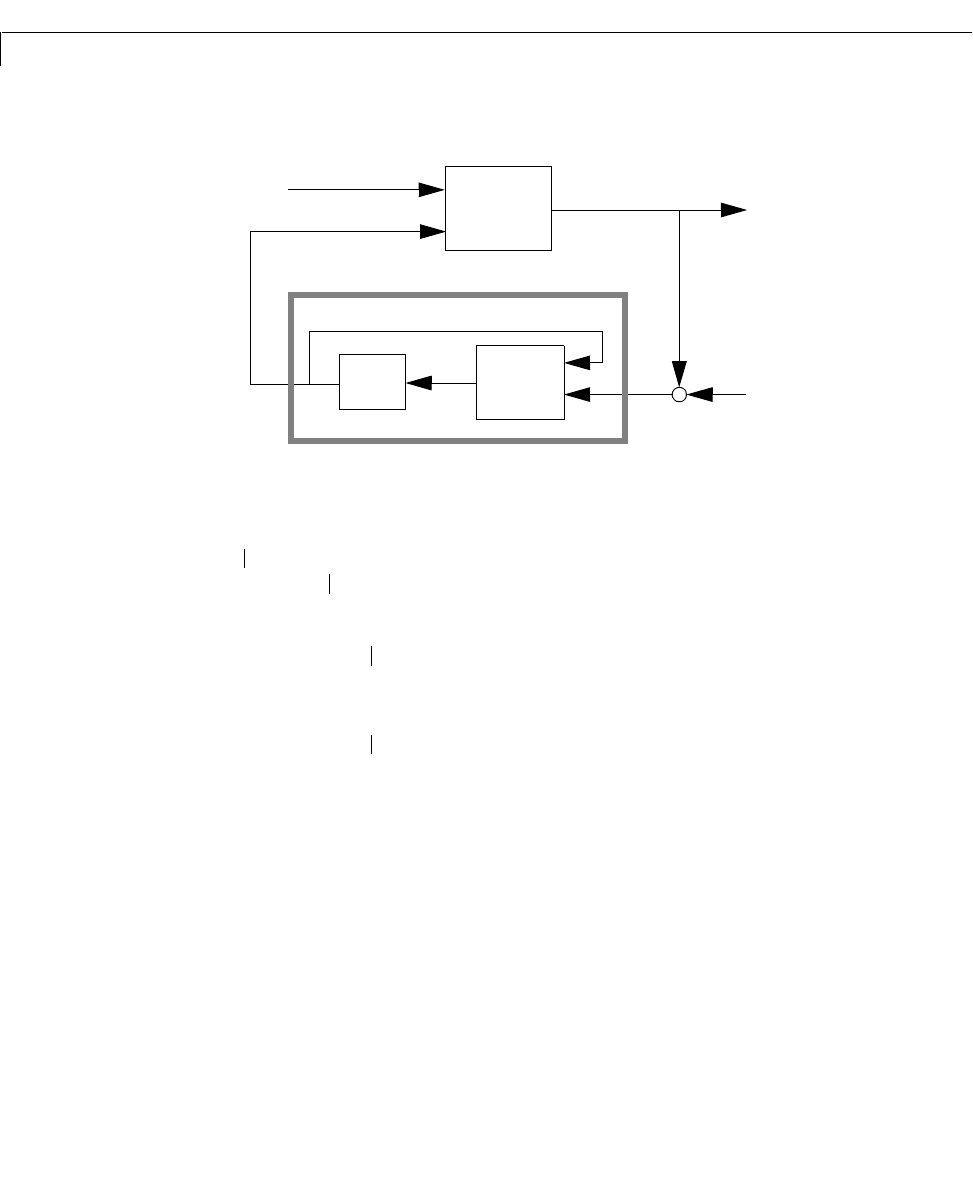
Usage rlqg = lqgreg(kest,k) returnsthe LQG regulator rlqg (a state-space model)
given the Kalman estimator
kest and the state-feedback gain matrix k.The
same function handles both continuous- and discrete-time cases. Use
consistent tools to design
kest and k:
u
y
+
+
x
ˆ
K–
LQG regulator
u
Plant
Measurement
noise
Kalman
filter
Process
noise
y
v
x
ˆ
nn 1–[]
xn
[]
y
v
n 1
–[]
x
ˆ
nn[]
y
v
n
[]
un[] Kx
ˆ
nn 1–[]–=
un[] Kx
ˆ
nn[]–=
IKMD
–
un
[]
y
v
n
[]