User`s guide

lft
11-115
11lft
Purpose Redheffer star product (linear fractional transformation) of two LTI models
Syntax sys = lft(sys1,sys2)
sys = lft(sys1,sys2,nu,ny)
Description lft formsthe star productor linear fractional transformation (LF T) of two LTI
models or LTI arrays. Such interconnections are widely used in robust control
techniques.
sys = lft(sys1,sys2,nu,ny) forms t he star product sys of the two LTI
models (or LTI arrays)
sys1 and sys2. The star product amounts to the
following feedback connection for single LTI models (or for each model in an
LTI array).
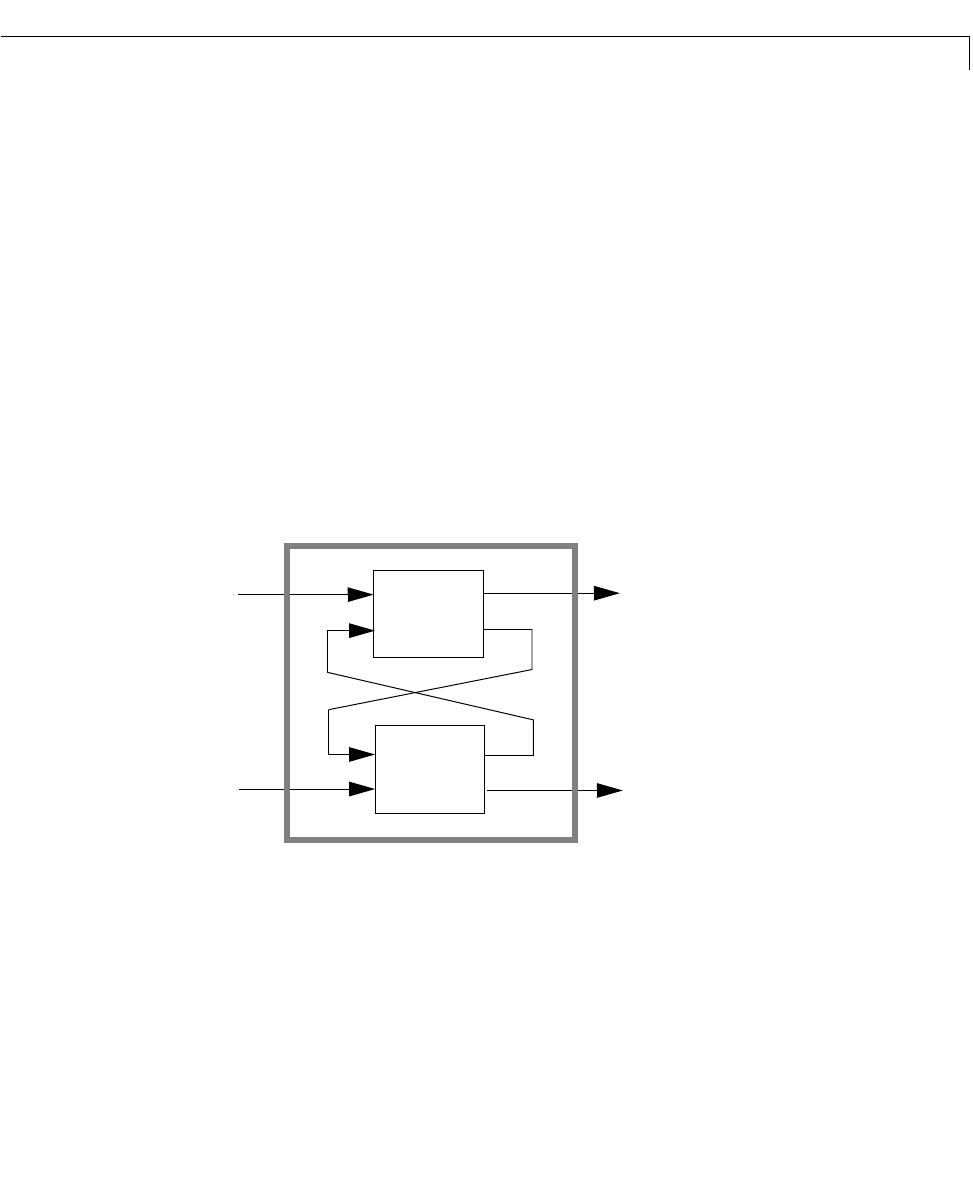
This feedback loop connects the first
nu outputs of sys2 to the last nu inputs of
sys1 (signals ), and the last ny outputs of sys1 to the first ny inputs of sys2
(signals ). The resulting system sys maps the input vector to the
output vector .
sys1
sys2
sys
z
1
z
2
w
2
w
1
u
u
y
y
u
y
w
1
; w
2
[]
z
1
;z
2
[]