User`s guide

kalman
11-109
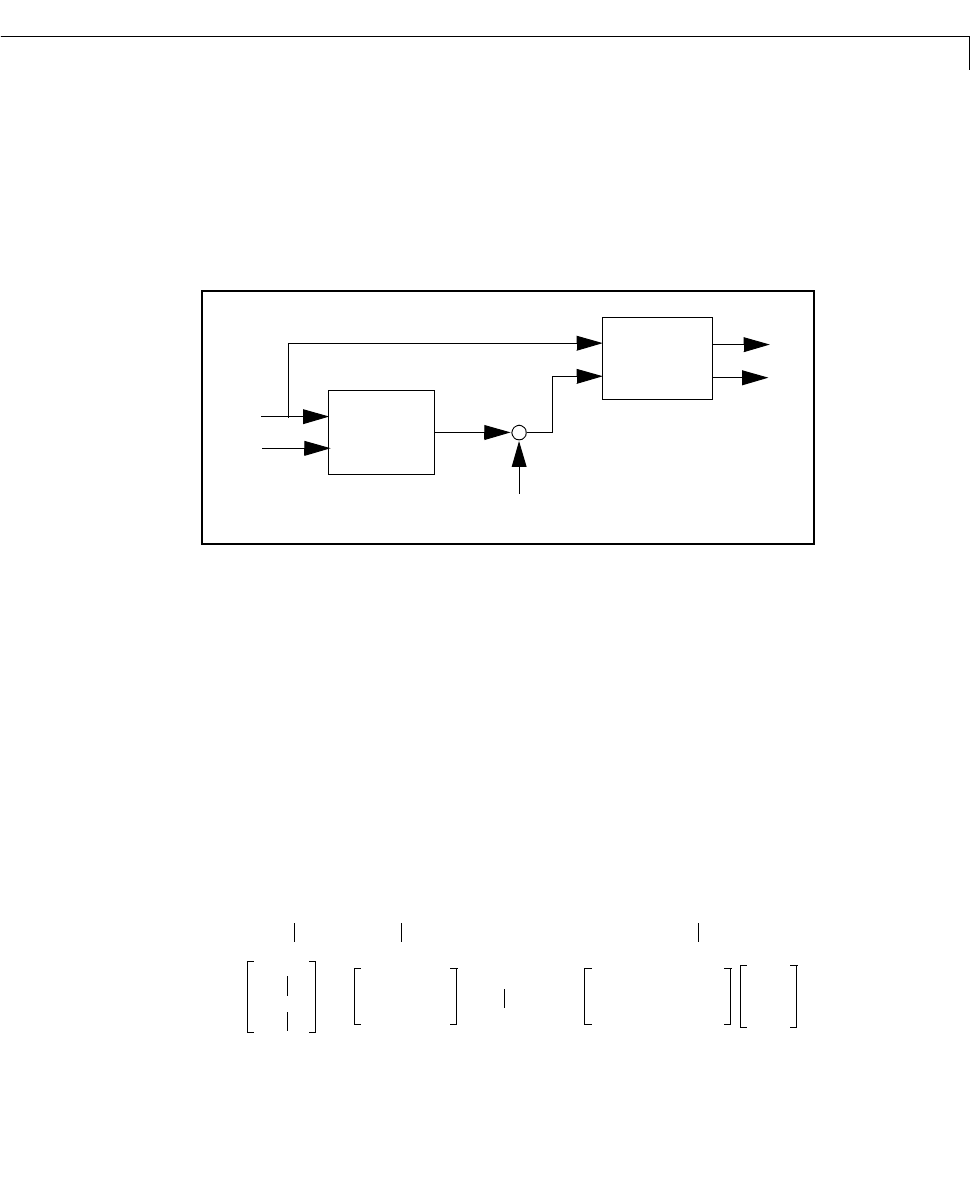
the output and state estimates and . Note that estimates the true plant
output
Discrete-Time Estimation
Given the discrete plant
and the noise covariance data
the Kalman estimator has equations
y
ˆ
x
ˆ
y
ˆ
yCxDuHw
++=
w
u
v
+
y
v
x
ˆ
Plant
y
Kalman
filter
u
y
ˆ
(Measurement noise)
Kalman estimator
xn 1
+[]
Ax n
[]
Bu n
[]
Gw n
[]++=
y
v
n[] Cx n[] Du n[] Hw n[] vn[]++ +=
Ewn[]wn[]
T
()Q,=Evn[]vn[]
T
()R=,Ewn[]vn[]
T
()N=
x
ˆ
n1n+[]Ax
ˆ
nn 1–[]Bu n[] Ly
v
n[] Cx
ˆ
nn 1–[]Du n[]––()++=
y
ˆ
nn[]
x
ˆ
nn[]
CI MC–()
IMC–
x
ˆ
nn 1–[]
ICM–()DCM
MD– M
un[]
y
v
n[]
+=