User`s guide

feedback
11-76
Example 2
Consider a state-space plant P with five inp uts and four outputs and a
state-spacefeedbackcontroller
K with threeinputsandtwo outputs.T o connect
outputs 1, 3, and 4 of the plant to the controller i nputs, and the controller
outputs to inputs 4 and 2 of the plant, use
feedin = [4 2];
feedout = [1 3 4];
Cloop = feedback(P,K,feedin,feedout)
Example 3
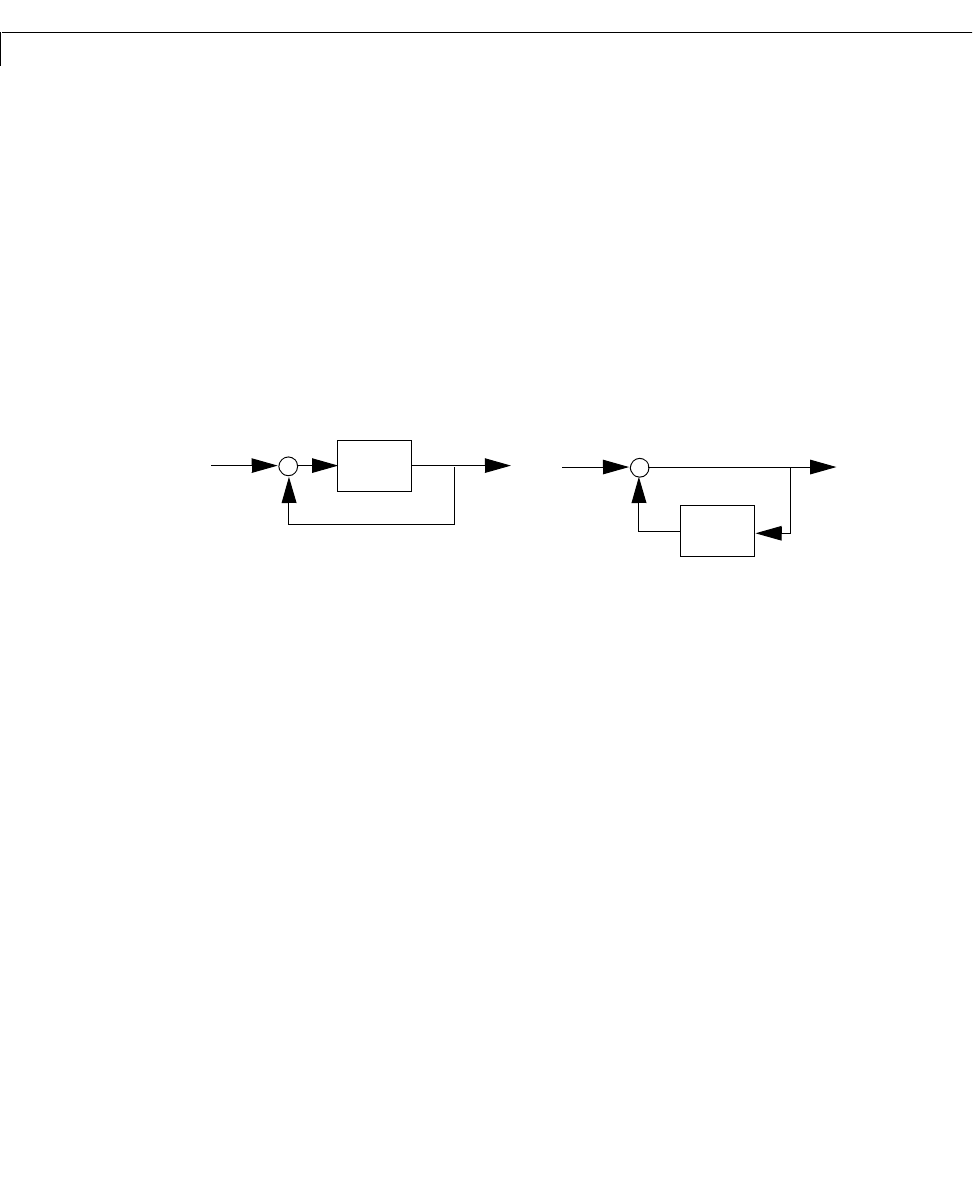
You can form the following negative-feedback loops
by
Cloop = feedback(G,1) % left diagram
Cloop = feedback(1,G) % right diagram
Limitations The feedback connection should be free of algebraic loop. If and are the
feedthrough m atrices of
sys1 and sys2, this condition is equivalent to:
• nonsingular when using negative feedback
• nonsingular when using positive feedback.
See Also star Star product of LTI systems (LFT connection)
series Series connection
parallel Paral lel connection
connect Derive state-space model for block diagram
interconnection
G
G
D
1
D
2
ID
1
D
2
+
ID
1
D
2
–