User`s guide

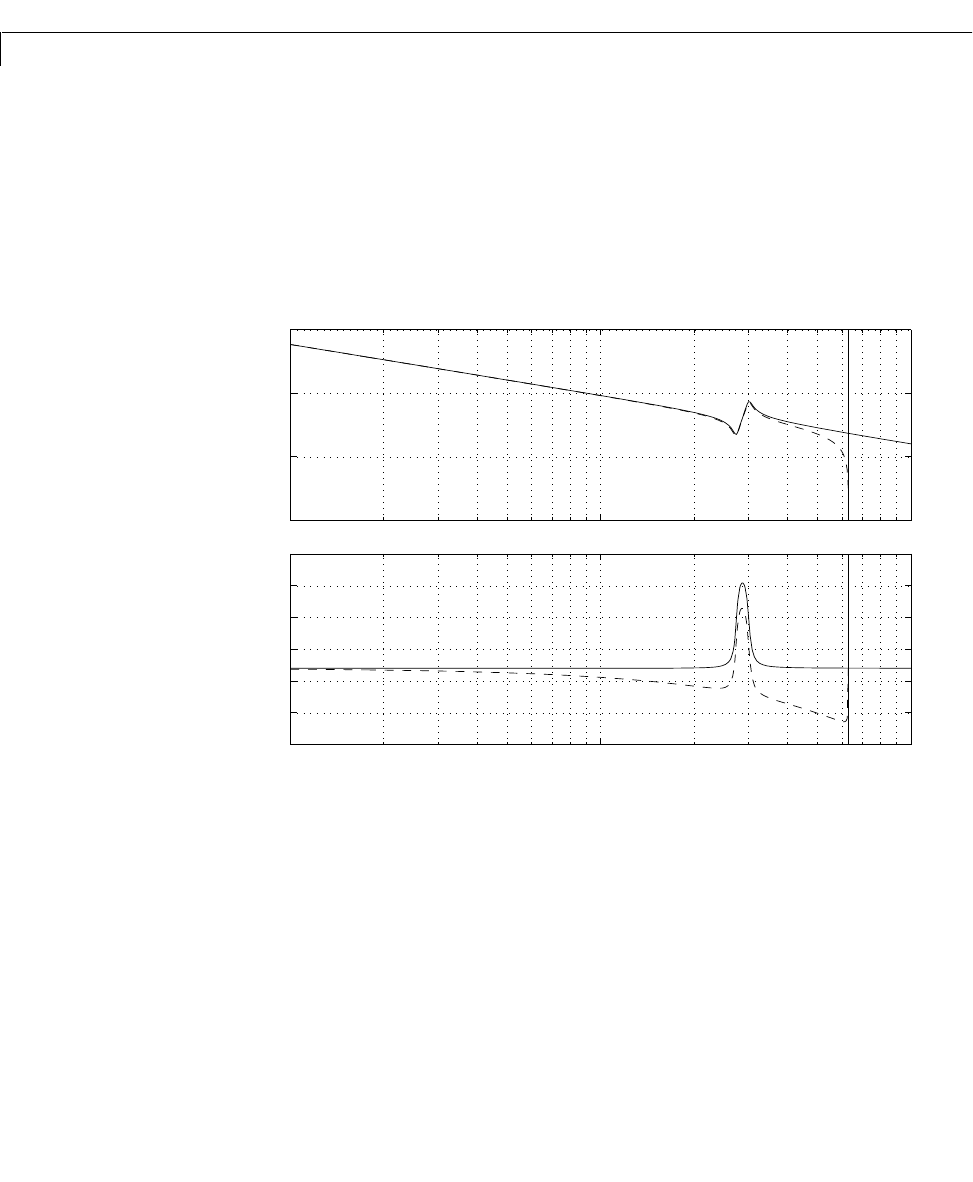
bode
11-22
You can also discretize this system using zero-order hold and the sample time
second, and compare the continuous and discretized responses by
typing
gd = c2d(g,0.5)
bode(g,'r',gd,'b--')
Algorithm For continuous-time systems, bode computes t he frequency response by
evaluating the transfer function on the imaginary axis . Only
positive frequencies are considered. For state-space models, the frequency
response is
When numerical ly safe, is diagonalized for maximum speed. Otherwise,
is reduced to upper Hessenberg form and the linear equation
is solved at each frequency point, taking advantage of the Hessenberg
T
s
0.5
=
Frequency (rad/sec)
Phase (deg); Magnitude (dB)
Bode Diagrams
−100
−50
0
50
10
−1
10
0
10
1
−300
−250
−200
−150
−100
−50
0
Hs
()
sj
ω=
ω
DCjωA–()
1
–
B+ ,ω0≥
A
A
j
ω
A
–()
XB
=