User`s guide

9 Design Case Studies
9-52
This is done by
% Note: set sample time to –1 to mark model as discrete
Plant = ss(A,[B B],C,0,–1,'inputname',{'u' 'w'},...
'outputname','y');
Assuming that , you can now design the discrete Kalman filter by
Q = 1; R = 1;
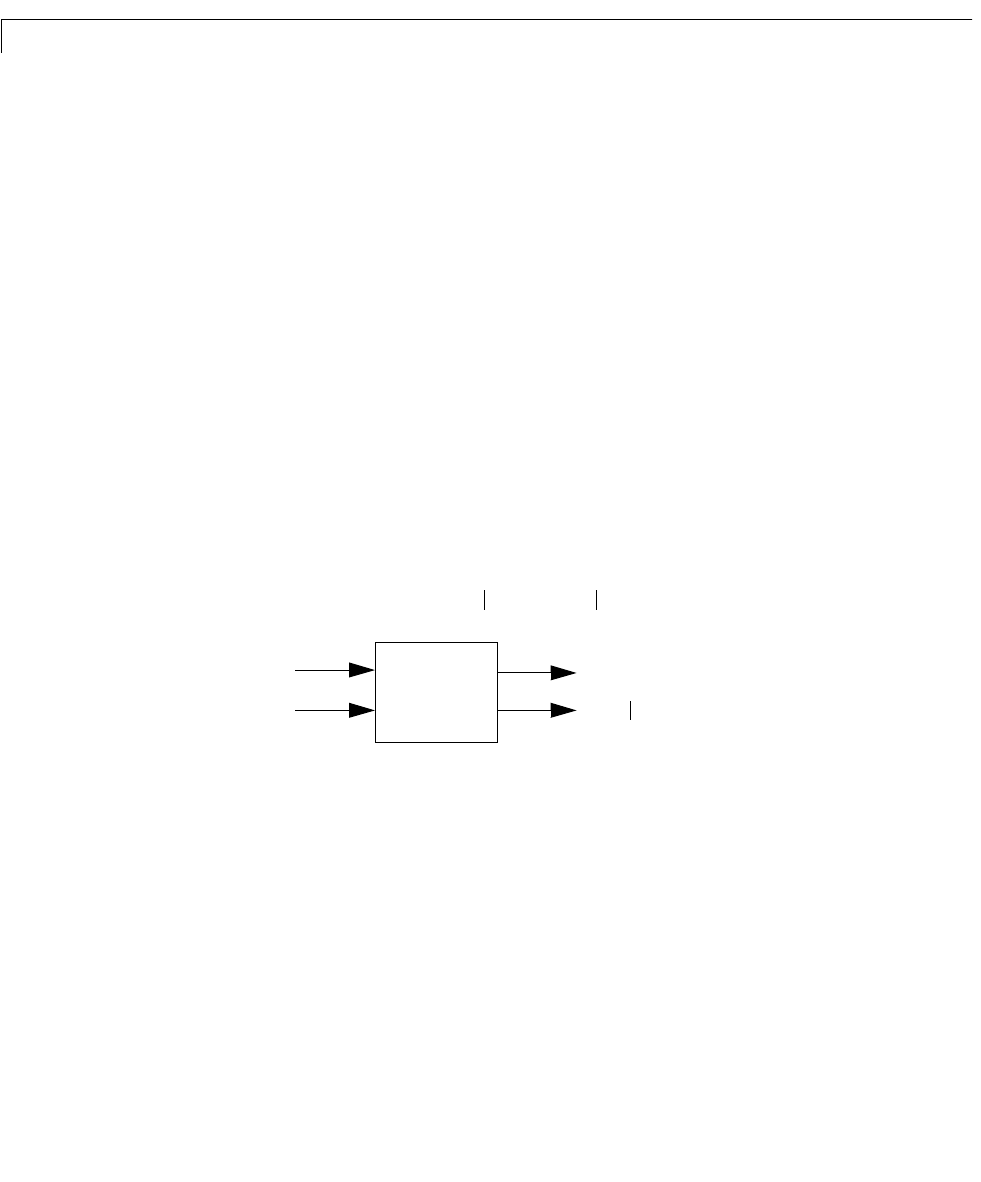
[kalmf,L,P,M] = kalman(Plant,Q,R);
This returns a state-space model kalmf of the filter as well as the innovation
gain
M
M =
3.7980e–01
8.1732e–02
–2.5704e–01
The inputs of kalmf are and , and its outputs are the plant output and
state estimates and .
QR1
==
u
y
v
y
e
y
ˆ
nn[]= x
ˆ
nn[]
kalmf
Kalman filter
u
x
ˆ
nn[]
y
v
y
e