User`s guide

Table Of Contents

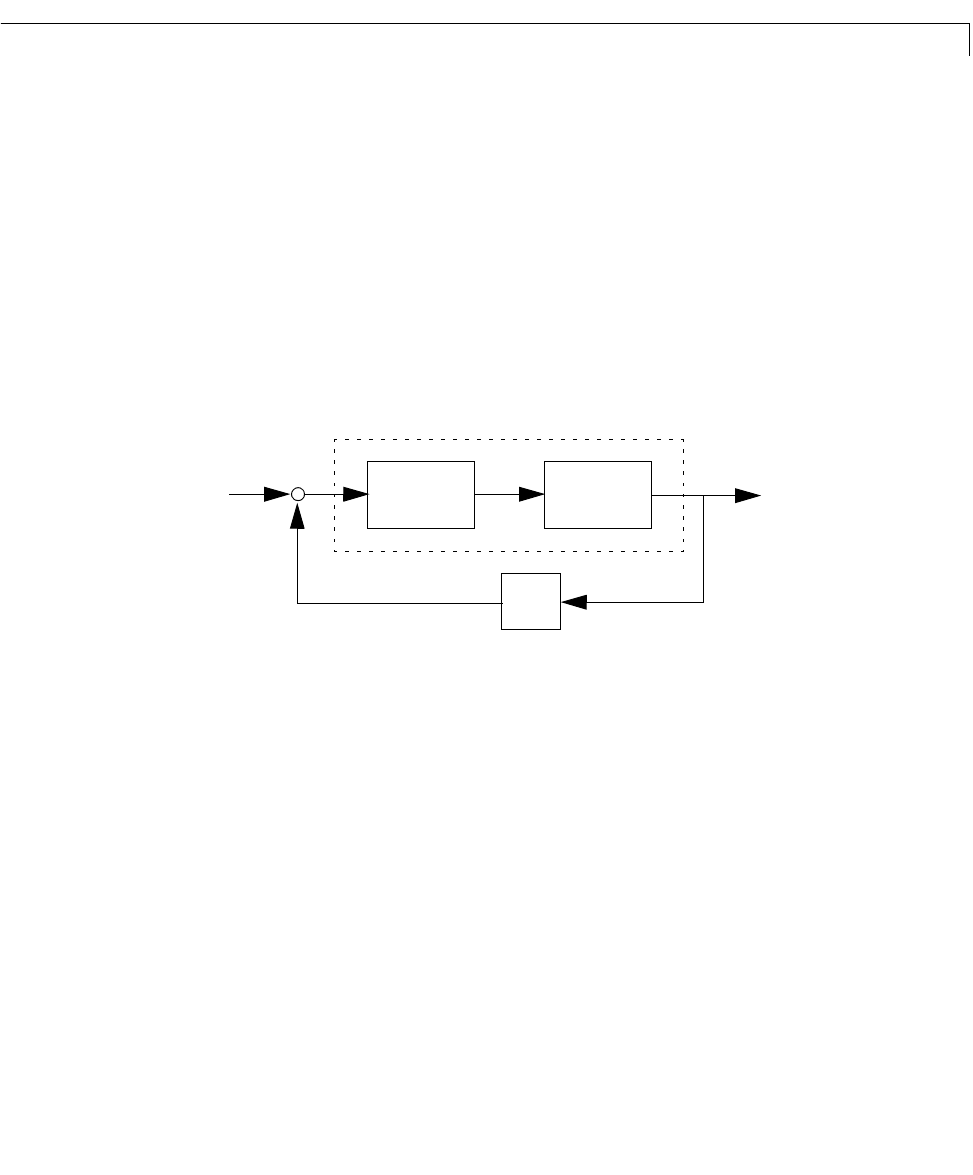
Hard-Disk Read/Write Head Controller

9-29

Now look at the robustness of your design. The m ost common classical

robustness criteriaare the gain andphase margins. Use the function

margin to

determinethesemargins.Withoutputarguments,

margin returnsthe gainand

phase margins as well as the corresponding crossover frequencies. Without

output argument,

margin plots the Bode response and displays the margins

graphically.

To compute the margins, first f orm the unity-feedback open loop by connecting

the compensator , plant model, and feedback gain in series.

olk = k * oloop;

Next apply margin to this open-loop model. Type

[Gm,Pm,Wcg,Wcp] = margin(olk);

Margins = [Gm Wcg Pm Wcp]

Margins =

3.7809 295.3172 43.1686 106.4086

To obtain the gain margin in dB, type

20*log10(Gm)

ans =

11.5760

You can also display the margins graphically by typing

margin(olk)

()

Dz()

Plant

–

oloop