User`s guide

7 Control Design Tools
7-8
LQG Design
Linear-Quadratic-Gaussian (LQG) control is a modern state-space technique
fordesigning optimal dynamic regulators. It enables you to trade off regulation
performance and control e ffort, and to take into account process and
measurement noise. Like pole placement, LQG design requires a state-space
model of the plant (use
ss to convert other LTI models to state space). This
sectionfocusesonthecontinuous-timecase(seerelatedReferencepagesfor
details on discrete-time LQG design).
LQG design addresses the following regulation problem.
The goal is to regulate the output around zero. The plant is driven by the
process noise and the controls , and the regulator relies on the noisy
measurements to generate these controls. The plant state and
measurement equati ons are of the form
and both and are modeled as white noise.
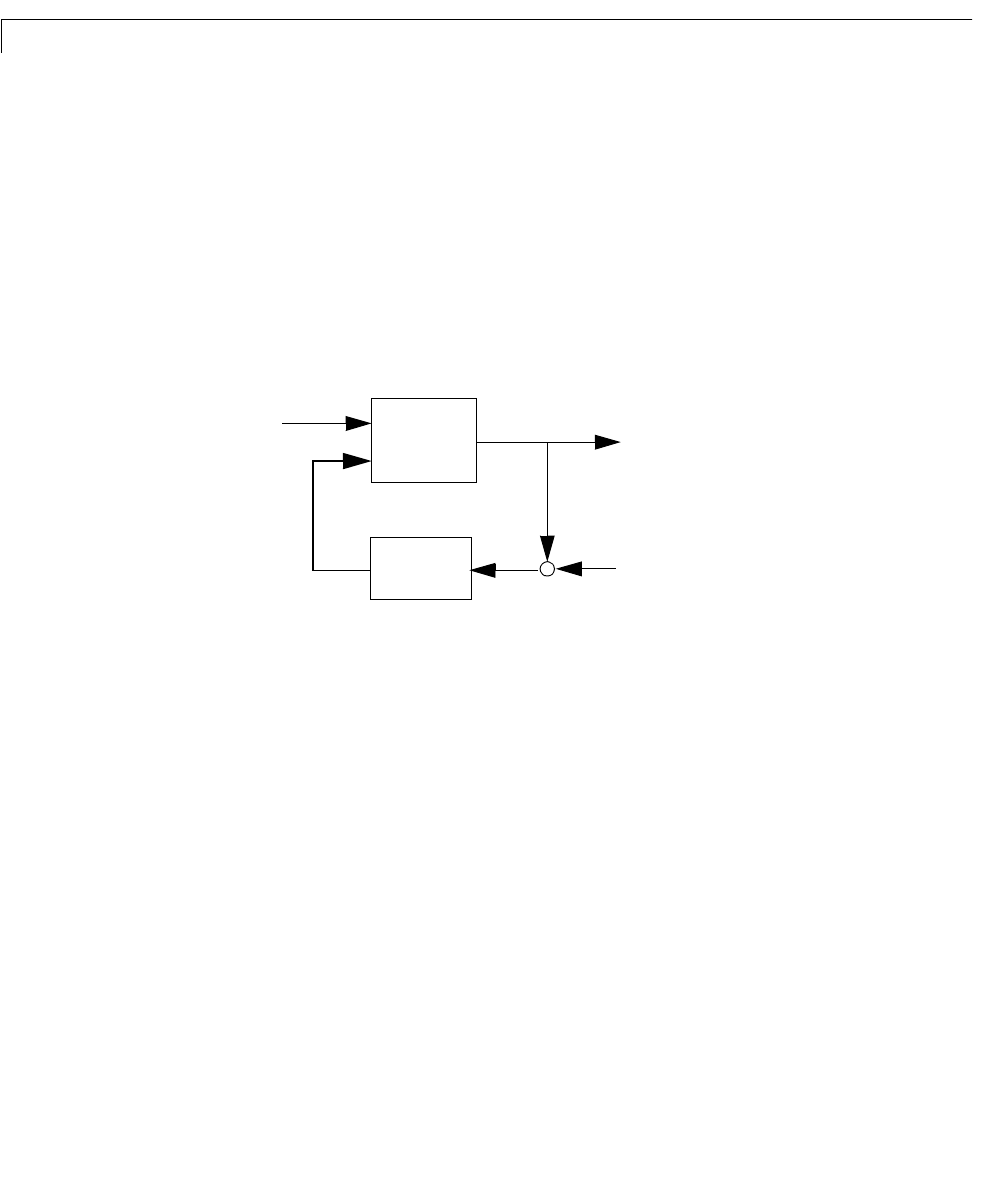
The LQG regulator consists of an optimal state-feedback gain and a Kalman
state estimator.You candesignt hesetwo componentsindependentlyas shown
next.
w
u
y
v
+
+
y
v
Plant
Regulator
y
w
u
y
v
yv
+=
x
·
Ax Bu Gw++=
y
v
Cx Du Hw v++ +=
w
v