Specifications

kalman
16-110
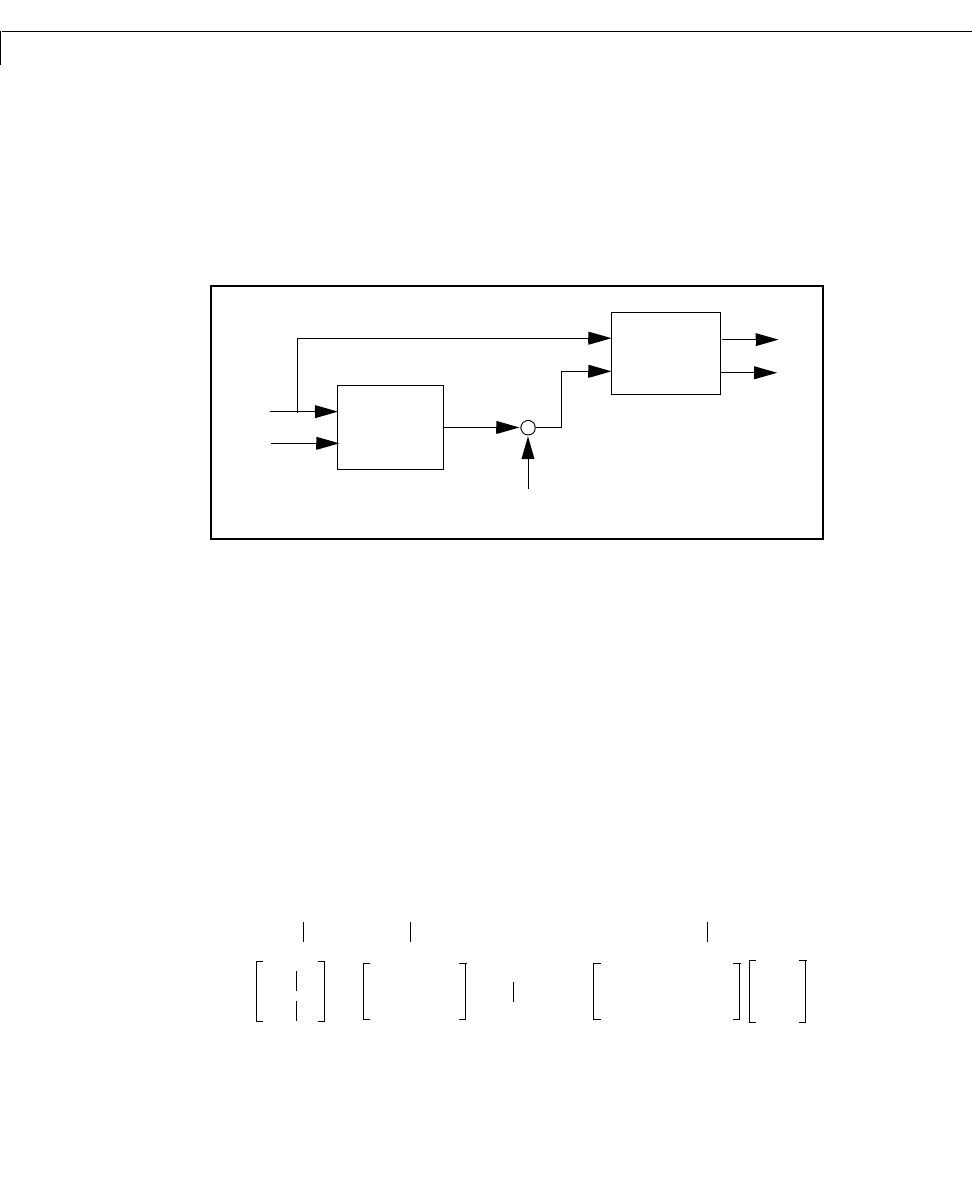
the output and state estimates and . Note that estimates the true plant
output
Discrete-Time Estimation
Given the discrete plant
and the noise covariance data
the Kalman estimator has equations
y x y
yCxDuHw++=
w
u
v
+
y
v
x
ˆ
Plant
y
Kalman
filter
u
y
ˆ
(Measurement noise)
Kalman estimator
xn 1+
[]
Ax n
[]
Bu n
[]
Gw n
[]
++=
y
v
n
[]
Cx n
[]
Du n
[]
Hw n
[]
vn
[]
++ +=
Ewn
[]
wn
[]
T
()
Q ,= Evn
[]
vn
[]
T
()
R= , Ewn
[]
vn
[]
T
()
N=
x
ˆ
n 1 n+
[]
Ax
ˆ
nn 1–
[]
Bu n
[]
Ly
v
n
[]
Cx
ˆ
nn 1–
[]
Du n
[]
––
()
++=
y
ˆ
nn[]
x
ˆ
nn[]
CI MC–()
IMC–
x
ˆ
nn 1–[]
ICM–()DCM
MD– M
un[]
y
v
n[]
+=