Specifications

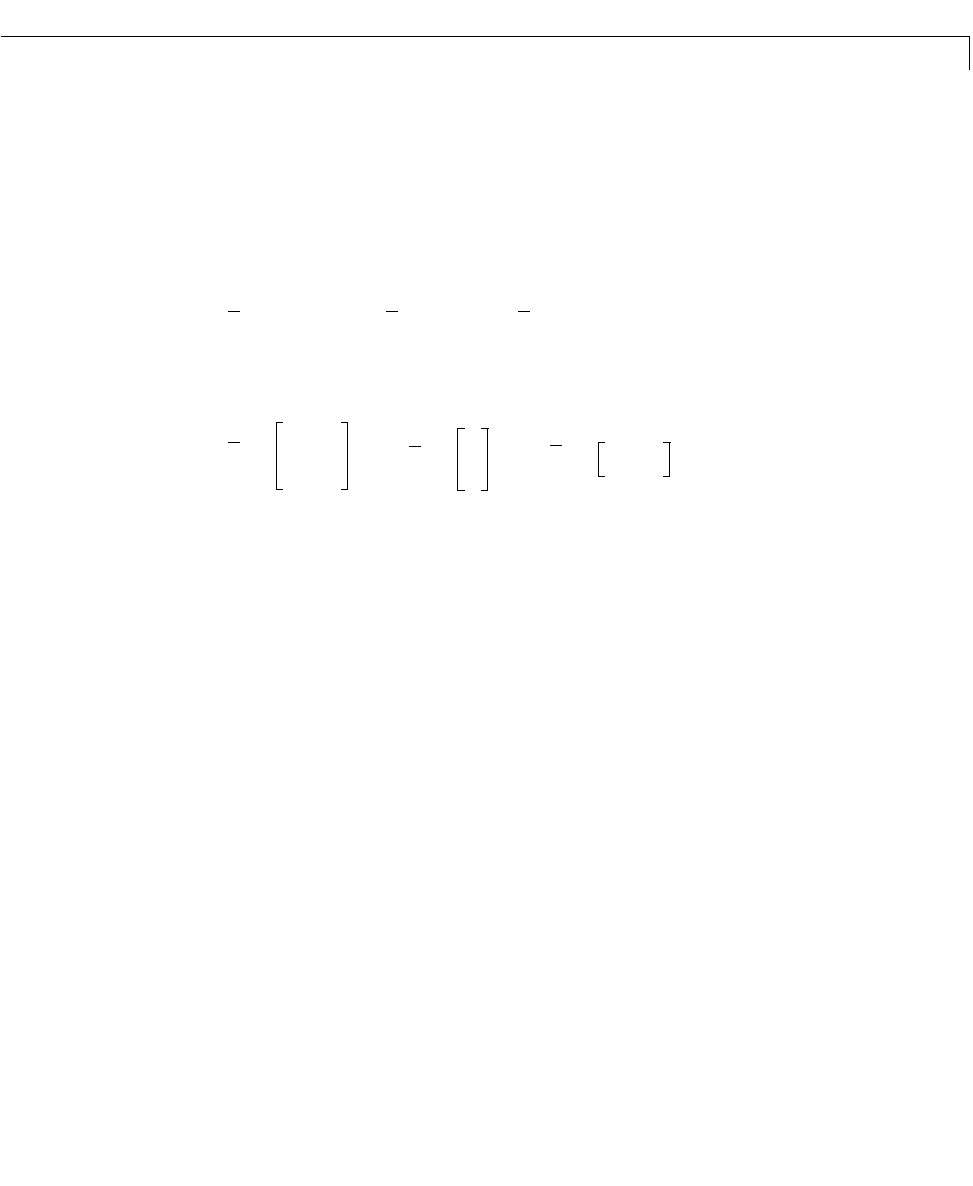
ctrbf
16-47
16ctrbf
Purpose Compute the controllability staircase form
Syntax [Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C)
[Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C,tol)
Description If the controllability matrix of has rank , where n is the size of
, then there exists a similarity transformation such that
where isunitary,and the transformed systemhasastaircaseform, in which
the uncontrollable modes, if there are any, are in the upper left corner.
where is controllable, all eigenvalues of are uncontrollable, and
[Abar,Bbar,Cbar,T,k] = ctrbf(A,B,C) decomposes the state-space system
represented by
A, B,andC into the controllability staircase form, Abar, Bbar,
and
Cbar, described above. T is the similarity transformation matrix and k is a
vector of length n,wheren is the order of the system represented by
A.Each
entryof
k representsthenumberofcontrollable states factored outduringeach
stepofthe transformationmatrixcalculation. Thenumberofnonzero elements
in
k indicates how many iterations werenecessary to calculate T, and sum(k) is
the number of states in , the controllable portion of
Abar.
ctrbf(A,B,C,tol) uses the tolerance tol when calculating the controllable/
uncontrollable subspaces. When the tolerance is not specified, it defaults to
10*n*norm(A,1)*eps.
Example Compute the controllability staircase form for
A =
1 1
4 -2
AB
,()
rn
≤
A
ATAT
T
,= BTB,= CCT
T
=
T
A
A
uc
0
A
21
A
c
,=
B
0
B
c
,= C
C
nc
C
c
=
A
c
B
c
,()
A
uc
C
c
sI A
c
–
()
1–
B
c
CsI A–
()
1–
B.=
A
c