Specifications

Building LTI Arrays
5-13
Suppose, based on measured input and output data, you estimate confidence
intervals , and for each of the parameters, and . All of the
possible combinations of the confidence limits for these model parameter
values give rise to a set of four SISO models.
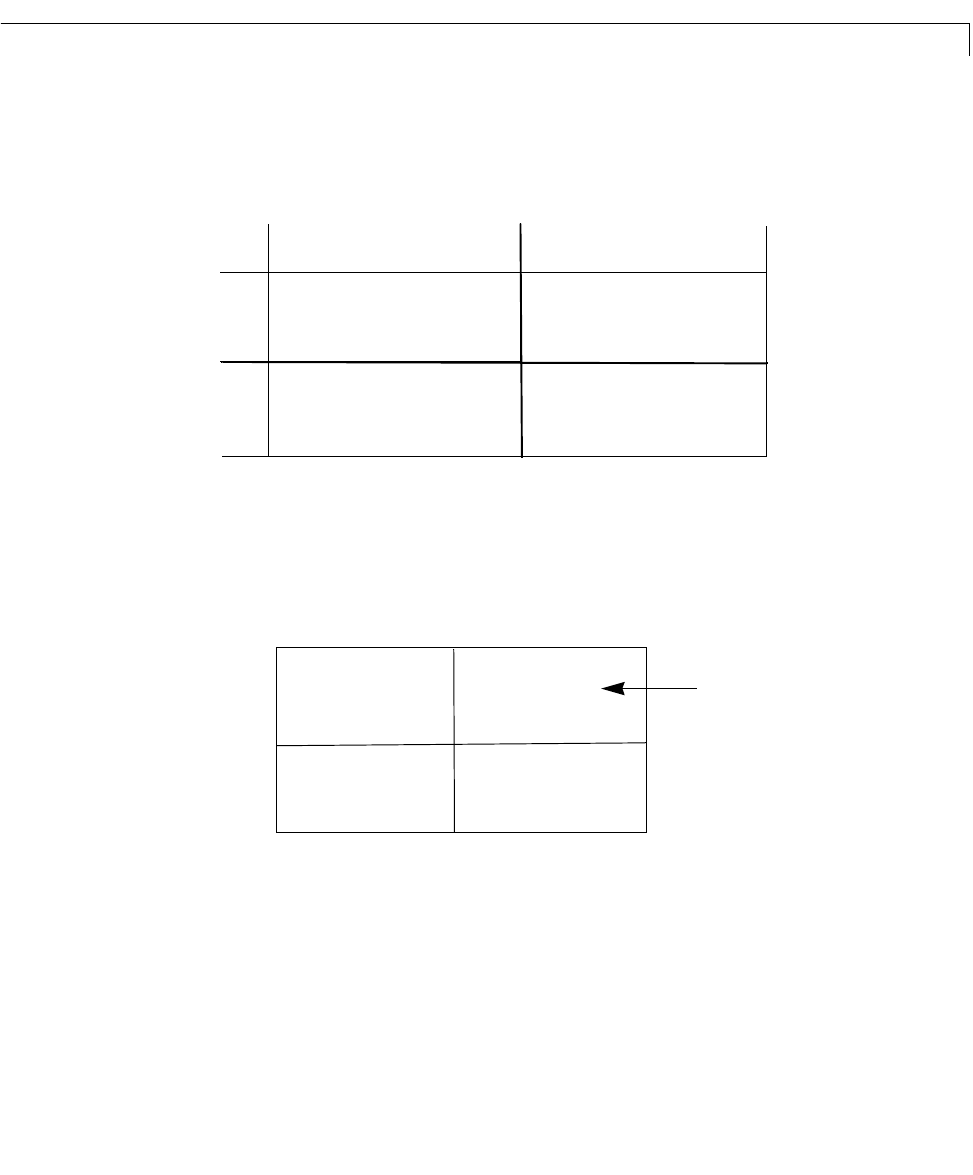
Figure 5-6: Four LTI Models Depending on Two Parameters
You can arrange these four models in a 2-by-2array of SISO transfer functions
called
H.
Figure 5-7: The LTI Array H
Here, for , represents the transfer function
corresponding to the parameter values and .
ω
1
ω
2
[,] ζ
1
ζ
2
[,] ω
ζ
H
11
s
()
ω
1
2
s
2
2
ζ
1
ω
1
s
ω
1
2
++
---------------------------------------------
=
H
21
s
()
ω
2
2
s
2
2
ζ
1
ω
2
s
ω
2
2
++
---------------------------------------------
=
H
22
s
()
ω
2
2
s
2
2
ζ
2
ω
2
s
ω
2
2
++
---------------------------------------------
=
H
12
s
()
ω
1
2
s
2
2
ζ
2
ω
1
s
ω
1
2
++
---------------------------------------------
=
ω
1
ω
2
ζ
1
ζ
2
H(:,:,1,1)
H(:,:,1,2)
H(:,:,2,1)
H(:,:,2,2)
ω
1
ω
2
ζ
2
ζ
1
Each entry of this 2-by-2 array is
a SISO transfer function model.
i,j 12
,{}∈
H(:,:,i,j)
ω
j
2
s
2
2ζ
i
ω
j
s ω
j
2
++
---------------------------------------------
ζζ
i
= ωω
j
=