HP-UX IPSec Version A.03.02.02 Administrator's Guide HP-UX 11i version 2 and HP-UX 11i version 3 (762800-001, April 2014)

The IKEv1 protocol specification requires Main Mode support; Aggressive Mode support is optional.
Aggressive Mode is required when IKE is used with autoconfiguration clients because these clients
do not have fixed IP addresses. Aggressive Mode enables IKE to select IKE parameters without
using the remote address in the IP packet header.
TIP: Most IPsec IKEv1 implementations, including HP-UX IPSec, use Main Mode by default.
The IKEv1 Phase 1 negotiation is also referred to as a Main Mode (MM ) or an Aggressive Mode
(AM ) negotiation, depending on the exchange type used.
Generating shared keys: Diffie-Hellman
IKE and IPsec SAs use shared keys to encrypt and authenticate communication. To be effective, a
shared key must be kept private, so other parties cannot decrypt the data or generate a valid
authentication code for modified data. This creates a challenge: How do the two parties agree on
the same shared key? How can you distribute the same key to both parties without exposing it to
other parties listening on the network?
One method for distributing shared keys is to use the Diffie-Hellman algorithm to dynamically
generate shared keys. The Diffie-Hellman algorithm enables two parties to establish a shared,
secret value while exchanging information over a nonsecure channel.
The Diffie-Hellman algorithm is based on the principle that (x^a)^b and (x^b)^a are both equivalent
to x^(a*b). With Diffie-Hellman key generation, each party generates two numbers: one public
and one private. These values are based on a selected, well-known numeric base, or Diffie-Hellman
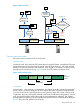
group. The two parties first select the same Diffie-Hellman group (Step 1 in Figure 8). The two
parties each select a public value and generate a mathematically related private value (Step 2 in
Figure 8). The two parties exchange public values (Step 3 in Figure 8). This exchange can occur
via a nonsecure channel. Each party then uses its private value and the other party’s public value
to generate a new value (Step 4 in Figure 8). Because of the mathematical properties of the numbers,
each party generates the same value, which can then be used as a shared key or use as a base
value to generate multiple shared keys.
Figure 8 Diffie-Hellman key generation
System A
System B
Step 1:
A and B agree on Diffie-
Hellman group
Step 2:
A and B each generate
public/private values
Step 3:
A and B exchange public
values with each other
Step 4:
A combines its private value
with B’s public value
B combines its private value
with A’s public value
A and B now have the same
shared secret value.
Public Value
Shared Secret
Value
Private
Value
Public Value
Private
Value
= =
IPsec protocol suite 39