User's Manual

20070201
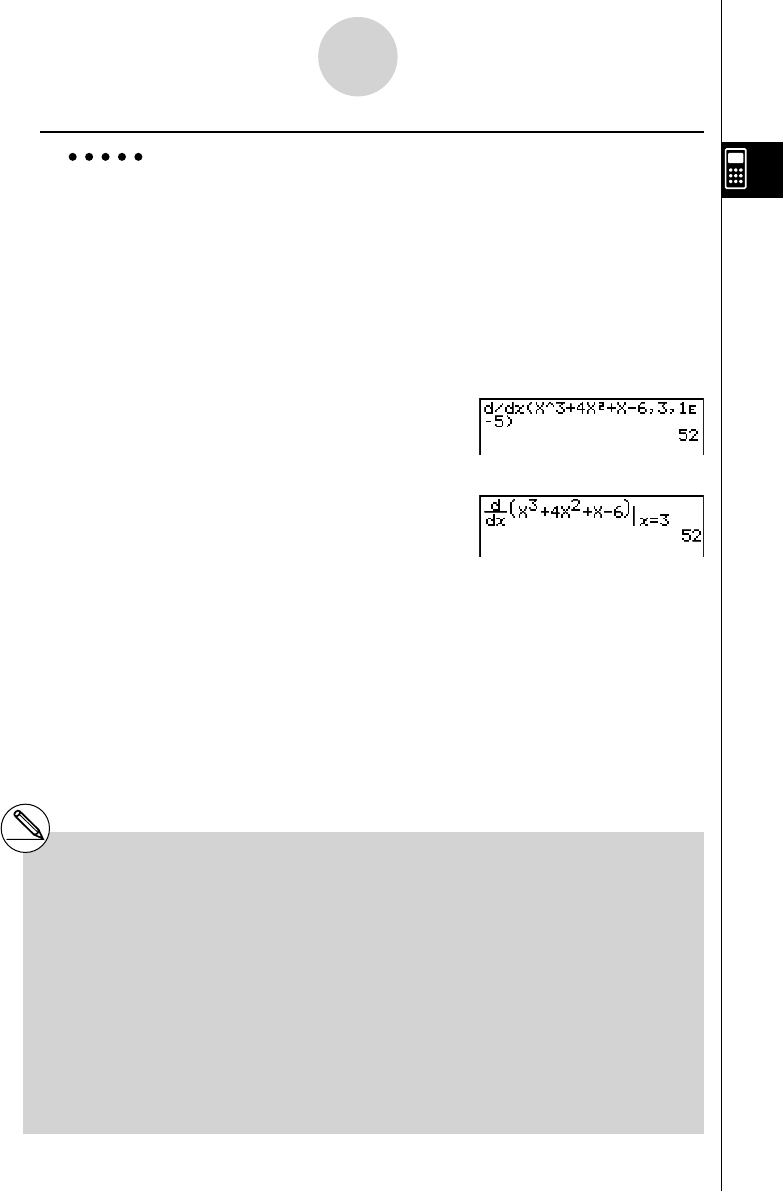
Example To determine the derivative at point
x = 3 for the function
y = x
3
+ 4 x
2
+ x – 6, with a tolerance of “ tol ” = 1 E – 5
Input the function
f ( x ).
A K 4 (CALC)2 (
d / dx )v M d+e vx + v -g,
Input point
x = a for which you want to determine the derivative.
d,
Input the tolerance value.
b E- f)
w
<Math>
A4 (MATH)4 (
d / dx )v M d e
+e vx + v -g e d
w
2-5-3
Numerical Calculations
# In the function f ( x ), only X can be used as
a variable in expressions. Other variables
(A through Z excluding X,
r , θ ) are treated
as constants, and the value currently
assigned to that variable is applied during the
calculation.
# Input of the tolerance (
tol ) value and the
closing parenthesis can be omitted. If you
omit tolerance (
tol ) value, the calculator
automatically uses a value for
tol as 1 E -10.
# Specify a tolerance (
tol ) value of 1E-14 or
greater. An error (Time Out) occurs whenever
no solution that satisfi es the tolerance value
can be obtained.
# In the Math input mode, the tolerance value is
fi xed at 1
E -10 and cannot be changed.
# Inaccurate results and errors can be caused by
the following:
- discontinuous points in
x values
- extreme changes in
x values
- inclusion of the local maximum point and local
minimum point in
x values
- inclusion of the infl ection point in
x values
- inclusion of undifferentiable points in
x values
- differential calculation results approaching zero