User's Manual

20070201
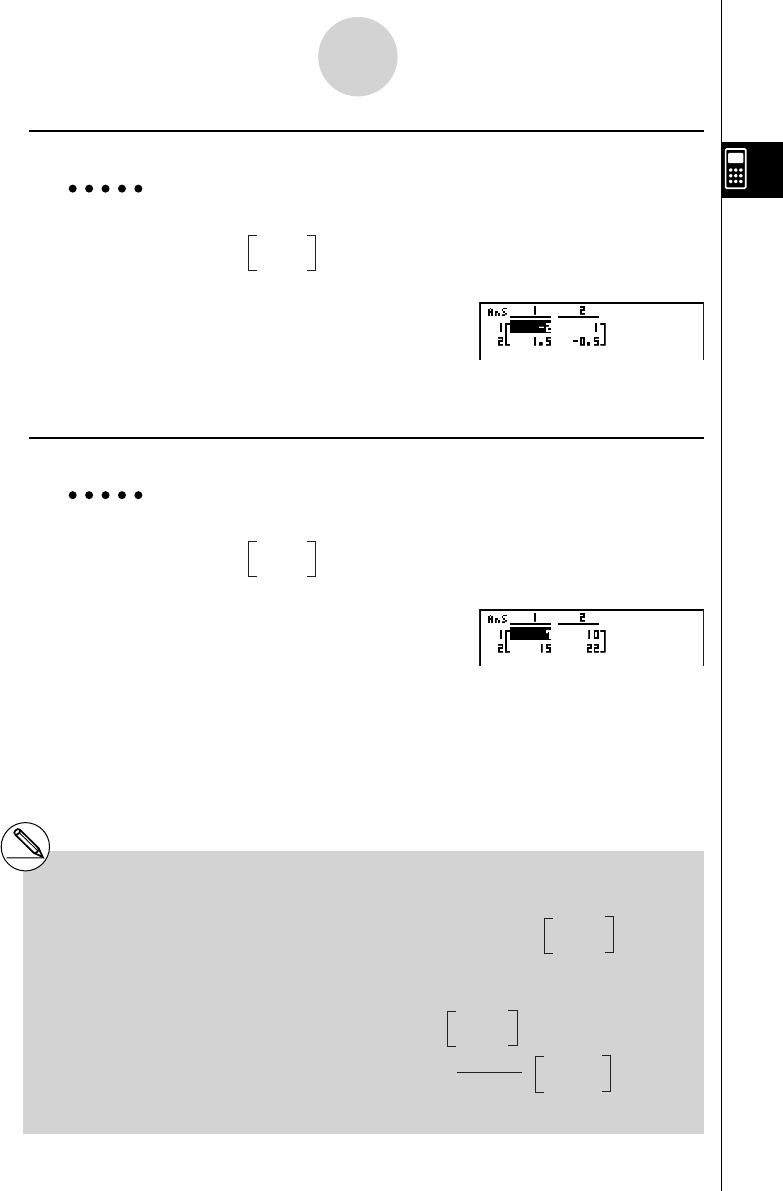
u Matrix Inversion [OPTN] - [MAT] - [ x
–1
]
Example To invert the following matrix :
Matrix A =
1 2
3 4
K 2 (MAT)1 (Mat)
av (A)! ) (
x
–1
)w
u Squaring a Matrix [OPTN] - [MAT] - [ x
2
]
Example To square the following matrix :
Matrix A =
1 2
3 4
K 2 (MAT)1 (Mat)av (A)xw
2-8-19
Matrix Calculations
# Only square matrices (same number of rows
and columns) can be inverted. Trying to invert
a matrix that is not square produces an error.
# A matrix with a determinant of zero cannot
be inverted. Trying to invert a matrix with
determinant of zero produces an error.
# Calculation precision is affected for matrices
whose determinant is near zero.
# A matrix being inverted must satisfy the
conditions shown below.
The following shows the formula used to
invert Matrix A into inverse matrix A
–1
.
Note that ad – bc
≠
0.
A A
–1
= A
–1
A = E =
1 0
0 1
A =
a b
c d
A
–1
=
1
ad – bc
d–b
–c a