User's Manual

20070201
u To input an identity matrix [OPTN] - [MAT] - [Iden]
Use the Identity command to create an identity matrix.
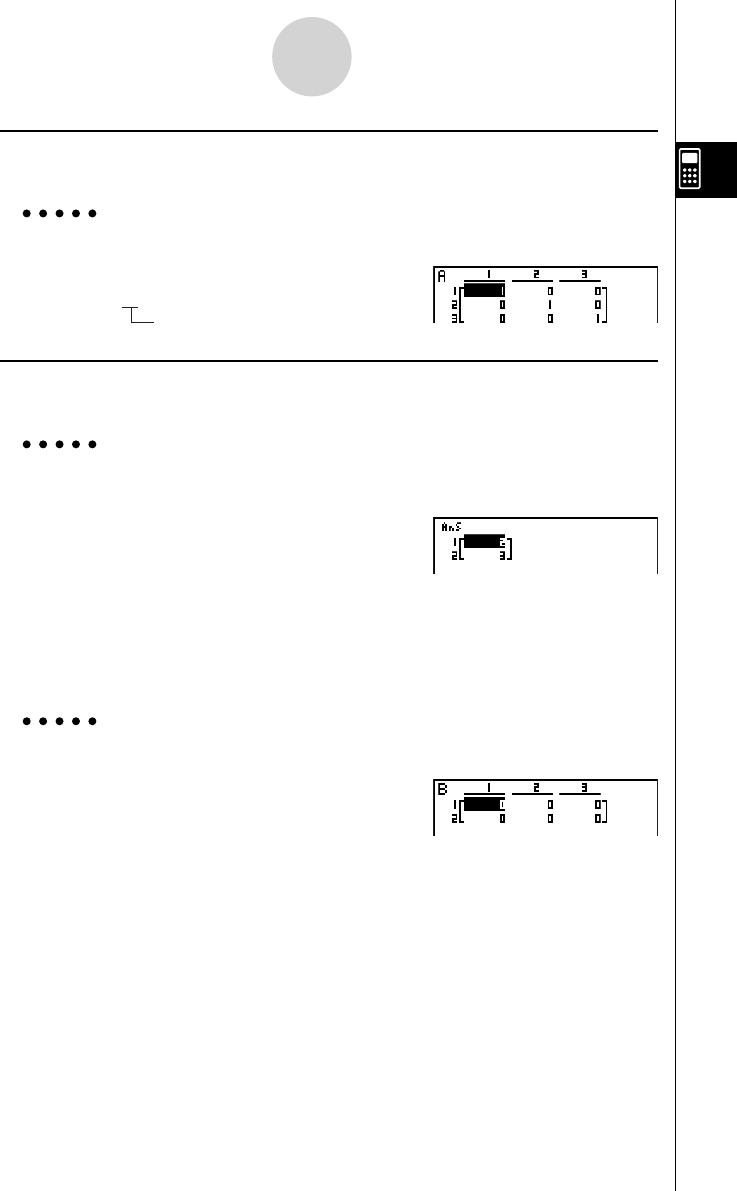
Example 2 To create a 3 × 3 identity matrix as Matrix A
K 2 (MAT)6 (g )1 (Iden)
d a 6 (g )1 (Mat)av (A)w
Number of rows/columns
u To check the dimensions of a matrix [OPTN] - [MAT] - [Dim]
Use the Dim command to check the dimensions of an existing matrix.
Example 3 To check the dimensions of Matrix A, which was input in
Example 1
K 2 (MAT)6 (g )2 (Dim)
6 (g )1 (Mat)av (A)w
The display shows that Matrix A consists of two rows and three columns.
Since the result of the Dim command is list type data, it is stored in ListAns memory.
You can also use {Dim} to specify the dimensions of the matrix.
Example 4 To specify dimensions of 2 rows and 3 columns for Matrix B
! * (  )c,d ! / (  )a
K 2 (MAT)6 (g )2 (Dim)
6 (g )1 (Mat)al (B)w
2-8-12
Matrix Calculations