User's Manual

20070201
2-6-3
Complex Number Calculations
# The result of the argument calculation differs
in accordance with the current angle unit
setting (degrees, radians, grads).
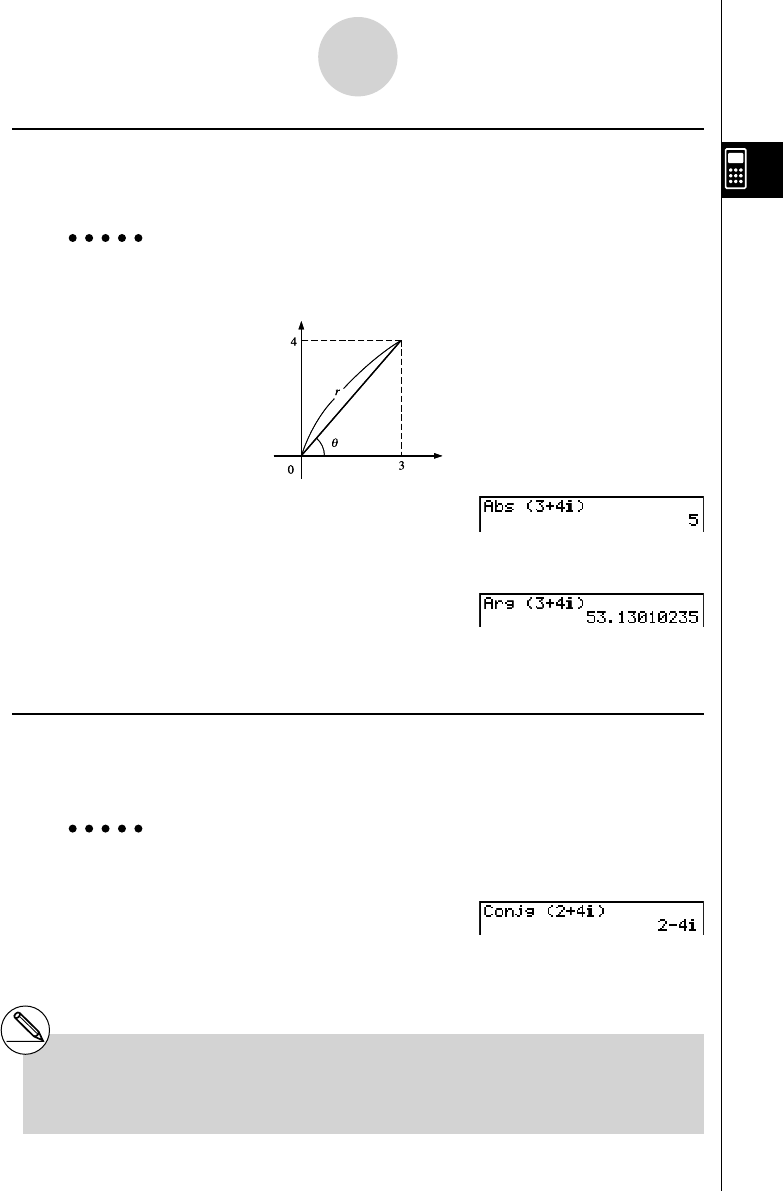
k Absolute Value and Argument [OPTN] - [CPLX] - [Abs]/[Arg]
The unit regards a complex number in the form a + b i as a coordinate on a Gaussian plane,
and calculates absolute value
⎮
Z
⎮
and argument (arg).
Example To calculate absolute value (
r ) and argument ( θ ) for the complex
number 3 + 4 i , with the angle unit set for degrees
Imaginary axis
Real axis
A K 3 (CPLX)2 (Abs)
(d+e 1 (
i )) w
(Calculation of absolute value)
A K 3 (CPLX)3 (Arg)
(d+e 1 ( i )) w
(Calculation of argument)
k Conjugate Complex Numbers [OPTN] - [CPLX] - [Conj]
A complex number of the form a + b i becomes a conjugate complex number of the form
a – b i .
Example To calculate the conjugate complex number for the complex number 2
+ 4
i
A K 3 (CPLX)4 (Conj)
(c+e 1 (
i )) w