User's Manual

20070201
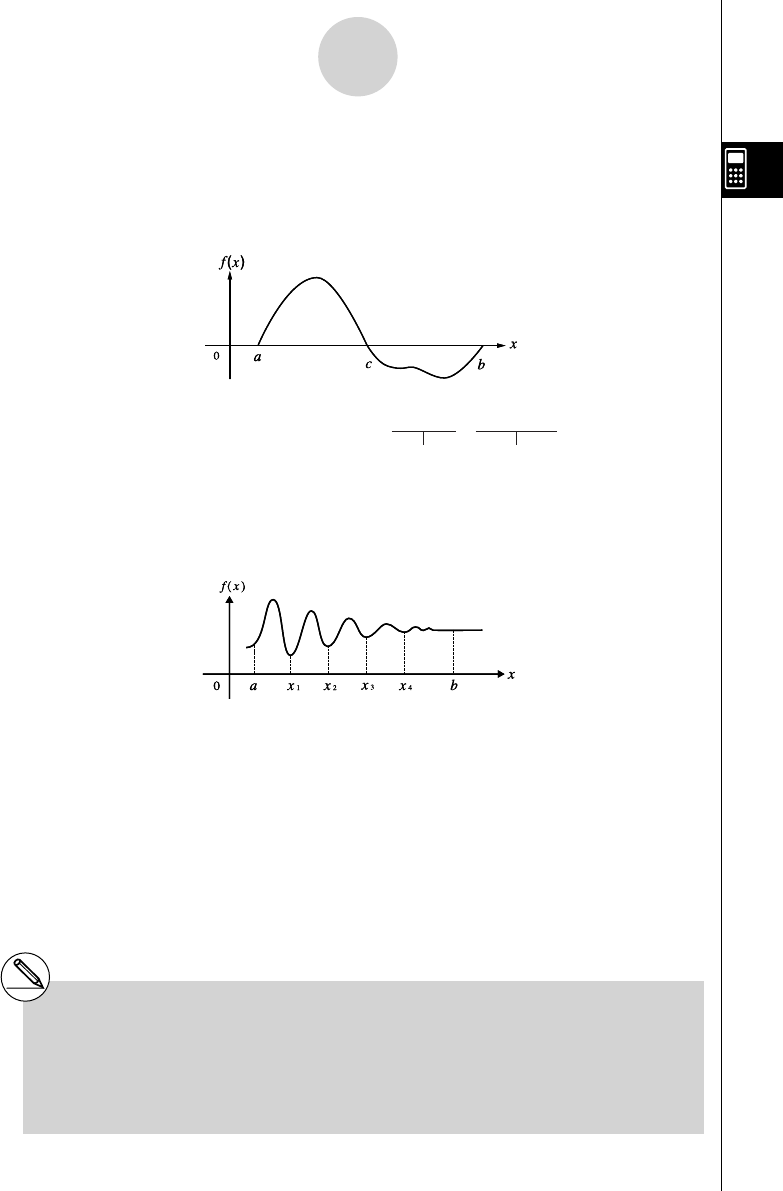
Note the following points to ensure correct integration values.
(1) When cyclical functions for integration values become positive or negative for different
divisions, perform the calculation for single cycles, or divide between negative and
positive, and then add the results together.
Positive
part (
S
)
Negative part (
S
)
Positive part ( S ) Negative part ( S )
(2) When minute fl uctuations in integration divisions produce large fl uctuations in integration
values, calculate the integration divisions separately (divide the large fl uctuation areas
into smaller divisions), and then add the results together.
∫
a
b
f
(
x
)
dx =
∫
a
c
f
(
x
)
dx
+ (–
∫
c
b
f
(
x
)
dx
)
∫
a
b
f
(
x
)
dx =
∫
a
c
f
(
x
)
dx
+ (–
∫
c
b
f
(
x
)
dx
)
∫
a
b
f
(
x
)
dx =
∫
a
x
1
f
(
x
)
dx
+
∫
x
1
x
2
f
(
x
)
dx
+.....+
∫
x
4
b
f
(
x
)
dx
∫
a
b
f
(
x
)
dx =
∫
a
x
1
f
(
x
)
dx
+
∫
x
1
x
2
f
(
x
)
dx
+.....+
∫
x
4
b
f
(
x
)
dx
2-5-9
Numerical Calculations
# Pressing A during calculation of an integral
(while the cursor is not shown on the display)
interrupts the calculation.
# Always use radians (Rad mode) as the
angle unit when performing trigonometric
integrations.
# An error (Time Out) occurs whenever no
solution that satisfi es the tolerance value can
be obtained.