Software Gebruiksaanwijzing

2-47
Matrix A =
K2(MAT) 6( g) 5(Rref)
6( g)1(Mat) av(A) w
• De operaties op rijen en herleide operaties op rijen leveren eventueel geen nauwkeurige
resultaten omwille van weggelaten cijfers.
u Inverse van een matrix [ x
−1
]
Voorbeeld Bereken de inverse matrix van de volgende matrix:
Matrix A =
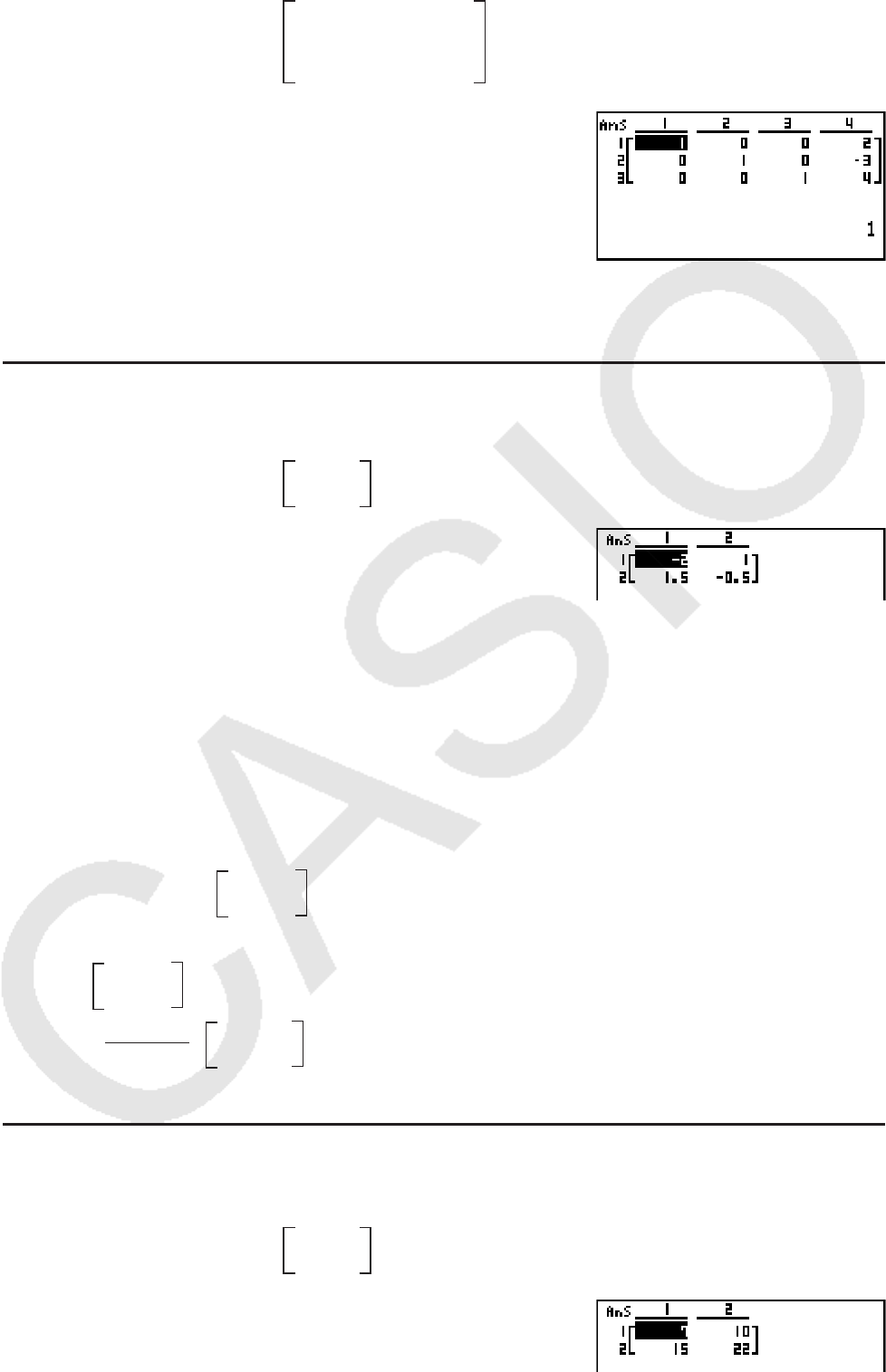
K2(MAT) 1(Mat)
av(A) !)(
x
–1
) w
• Alleen van een vierkante matrix (zelfde aantal rijen en kolommen) kan een inverse berekend
worden. Als u probeert de inverse van een niet-vierkante matrix te berekenen, verschijnt een
foutmelding.
• Een matrix waarvan de determinant 0 is, heeft geen inverse. Als u probeert de inverse van
zo’n matrix te berekenen, verschijnt een foutmelding.
• Van matrices waarvan de determinant bijna 0 is, zullen de inversen niet heel precies worden
berekend.
• Een inverse matrix heeft de volgende eigenschap:
A A
–1
= A
–1
A = E =
1 0
0 1
Een inverse matrix A
–1
van Matrix A wordt als volgt berekend:
A =
a b
c d
A
–1
=
1
ad – bc
d–b
–c a
Merk op dat ad – bc ≠ 0.
u Kwadraat van een vierkante matrix [ x
2
]
Voorbeeld Kwadrateer de volgende matrix:
Matrix A =
K2(MAT) 1(Mat) av(A) xw
2 −1 3 19
1 1 −5 −21
0 4 3 0
2 −1 3 19
1 1 −5 −21
0 4 3 0
1 2
3 4
1 2
3 4
1 2
3 4
1 2
3 4