Software Gebruiksaanwijzing

6-8
u Std
(1) Wanneer alle frequentiewaarden gehele getallen zijn
Met deze berekeningsmethode hangt het verwerken er van af of het aantal elementen
n in de
populatie een even of oneven getal is.
Als het aantal elementen
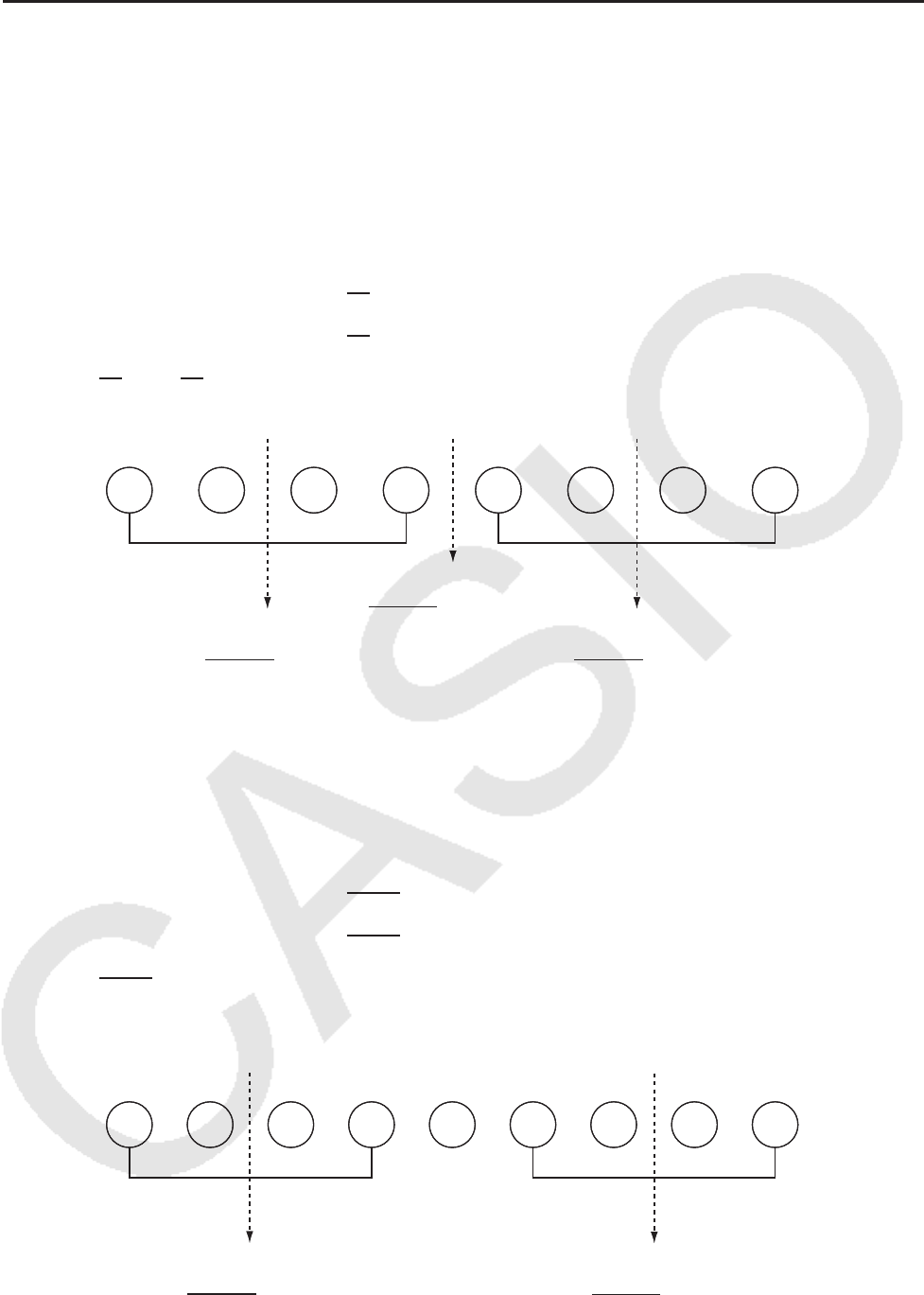
n een even getal is:
Met het middelpunt van de totale populatie als referentie, worden de elementen van de
populatie in twee groepen verdeeld: een groep van de onderste helft en een groep van de
bovenste helft. Q1, Q3 en Med worden dan de waarden die hieronder zijn beschreven.
Q1 = {mediaan van de groep van
2
n
items uit de onderkant van de populatie}
Q3 = {mediaan van de groep van
2
n
items uit de bovenkant van de populatie}
Med = {
2
n
-e en
2
n
+1-e element gemiddelde waarde}
Middelpunt Middelpunt Middelpunt
Als het aantal elementen n een oneven getal is:
Met de mediaan van de totale populatie als referentie, worden de elementen van de populatie
in twee groepen verdeeld: een onderste helft van de populatie (lagere waarden dan de
mediaan) en een bovenste helft van de populatie (hogere waarden dan de mediaan). De
waarde van de mediaan is niet meegerekend. Q1, Q3 en Med worden dan de waarden die
hieronder zijn beschreven.
Q1 = {mediaan van de groep van
2
n
– 1
items uit de onderkant van de populatie}
Q3 = {mediaan van de groep van
2
n
– 1
items uit de bovenkant van de populatie}
Med = {
2
n
+ 1
-e element}
• Als n = 1, Q1 = Q3 = Med = middelpunt van de populatie.
Middelpunt Middelpunt
2
4
+
5
=
Midden
= Q1
2
2
+
3
= Q3
2
6
+
7
12345678
2
4
+
5
=
Midden
= Q1
2
2
+
3
= Q3
2
6
+
7
12345678
Midden
1 234567 98
= Q1
2
2
+
3
= Q3
2
7
+
8
Midden
1 234567 98
= Q1
2
2
+
3
= Q3
2
7
+
8