User manual - fx-9860GII_Soft

4-2
 CU@UAU@U
@UEUBU@U
DUCU@UFU
 (SOLV)
• Interne beregninger udføres med en 15-cifret mantisse, men resultaterne vises med en
10-cifret mantisse og en 2-cifret eksponent.
• Flere lineære ligninger løses ved at invertere den matrix, der indeholder ligningernes
koefficienter. For eksempel, viser følgende illustration løsningen (
x, y, z) på en samtidig
lineær ligning med tre ubekendte.
Derfor mindskes præcisionen, når determinantens værdi er tæt på nul. Det kan desuden
tage lang tid at løse flere ligninger med tre eller flere ubekendte.
• Der opstår en fejl, hvis lommeregneren ikke kan finde en løsning.
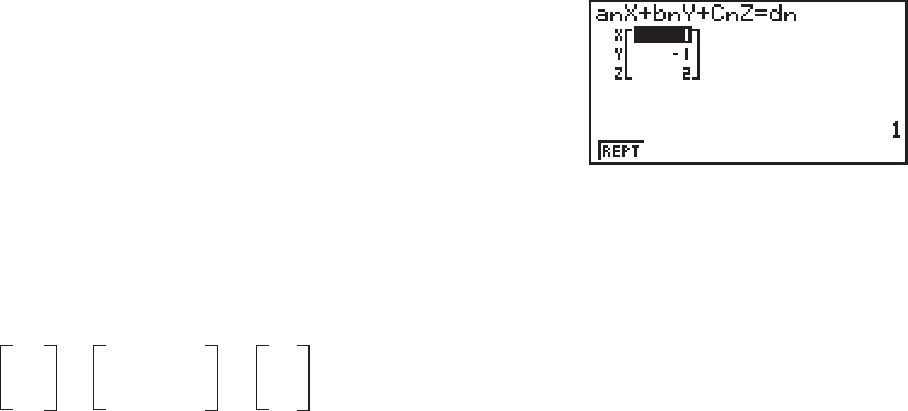
• Når beregningen er udført, kan du trykke på
(REPT), ændre koefficienternes værdier og
derefter udføre beregningen igen.
2. Højordensligninger fra 2. til 6. grad
Din lommeregner kan bruges til at løse højordensligninger fra 2. til 6. grad.
• Andengradsligning:
ax
2
+ bx + c = 0 (a p 0)
• Tredjegradsligning:
ax
3
+ bx
2
+ cx + d = 0 (a p 0)
• Fjerdegradsligning:
ax
4
+ bx
3
+ cx
2
+ dx + e = 0 (a p 0)
…
1. Skift til tilstanden EQUA fra hovedmenuen.
2. Vælg tilstanden POLY (polynomial), og angiv ligningens grad.
Du kan angive en grad mellem 2 til 6.
3. Angiv koefficienterne i rækkefølge.
• Den celle, der i øjeblikket er valgt til indtastning, er fremhævet. Hver gang du indtaster en
koefficient, flyttes markøren i denne rækkefølge:
a m b m c m …
• Du kan også indtaste brøkdele og værdier, der er tildelt til variable, som koefficienter.
• Du kan annullere den værdi, du indtaster for den aktuelle koefficient, ved at trykke på
)
til enhver tid, før du trykker på U for at gemme koefficientværdien. Koefficienten nulstilles
til den værdi, den havde, før du startede indtastningen. Du kan derefter indtaste en anden
værdi, hvis du vil det.
• Hvis du vil ændre værdien af en koefficient, som du allerede har gemt ved at trykke på
U, skal du flytte markøren til den koefficient, som du vil redigere. Indtast derefter den
værdi, du vil ændre den til.
• Hvis du trykker på
(CLR), nulstilles alle koefficienterne til nul.
4. Løs ligningerne.
–1
=
x
y
z
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
d
1
d
2
d
3
–1
=
x
y
z
a
1
b
1
c
1
a
2
b
2
c
2
a
3
b
3
c
3
d
1
d
2
d
3