User manual - fx-9860GII_Soft
Table Of Contents
- Indhold
- Kom hurtigt i gang — Læs dette først!
- Kapitel 1 Grundlæggende funktioner
- Kapitel 2 Manuelle beregninger
- 1. Grundlæggende beregninger
- 2. Specielle funktioner
- 3. Angivelse af vinkelenhed og visningsformat
- 4. Funktionsberegninger
- 5. Numeriske beregninger
- 6. Beregninger med komplekse tal
- 7. Binære, oktale, decimale og heksadecimale beregninger med heltal
- 8. Matrixberegninger
- 9. Beregninger af metriske omregninger
- Kapitel 3 Funktionen List
- Kapitel 4 Ligningsregning
- Kapitel 5 Tegning af grafer
- 1. Grafeksempler
- 2. Håndtering af et grafskærmbillede
- 3. Tegning af en graf
- 4. Lagring af en graf i billedhukommelsen
- 5. Tegning af to grafer i det samme skærmbillede
- 6. Manuel tegning af grafer
- 7. Brug af tabeller
- 8. Tegning af dynamiske grafer
- 9. Tegning af en graf for en rekursionsformel
- 10. Tegning af et keglesnit
- 11. Ændring af en grafs udseende
- 12. Funktionsanalyse
- Kapitel 6 Statistiske grafer og beregninger
- 1. Før udførelse af statistiske beregninger
- 2. Beregning og tegning af en graf for statistiske data med én variabel
- 3. Beregning og tegning af en graf for statistiske data med to variable
- 4. Udførelse af statistiske beregninger
- 5. Test
- 6. Konfidensinterval
- 7. Fordeling
- 8. Input- og Output-udtryk til tests, konfidensinterval, og fordeling
- 9. Statistisk formel
- Kapitel 7 Økonomiske beregninger (TVM)
- Kapitel 8 Programmering
- Kapitel 9 Regneark
- Kapitel 10 eActivity
- Kapitel 11 Hukommelsesstyring
- Kapitel 12 Systemstyring
- Kapitel 13 Datakommunikation
- Kapitel 14 Brug af SD-kort (kun fx-9860GII SD)
- Appendiks
- E-CON2 Application (English)
- 1 E-CON2 Overview
- 2 Using the Setup Wizard
- 3 Using Advanced Setup
- 4 Using a Custom Probe
- 5 Using the MULTIMETER Mode
- 6 Using Setup Memory
- 7 Using Program Converter
- 8 Starting a Sampling Operation
- 9 Using Sample Data Memory
- 10 Using the Graph Analysis Tools to Graph Data
- 11 Graph Analysis Tool Graph Screen Operations
- 12 Calling E-CON2 Functions from an eActivity
6-1717
• Lineær regression (ax + b) .............
(
a + bx) ............
• Andengradsregression ...................
• Tredjegradsregression ....................
• Fjerdegradsregression ...................
• Logaritmisk regression ...................
• Eksponentiel regression (
a·e
bx
) .......
(
a·b
x
)........
• Regression opløftet til potens .........
• Sinusformet regression ..................
• Logistisk regression ........................
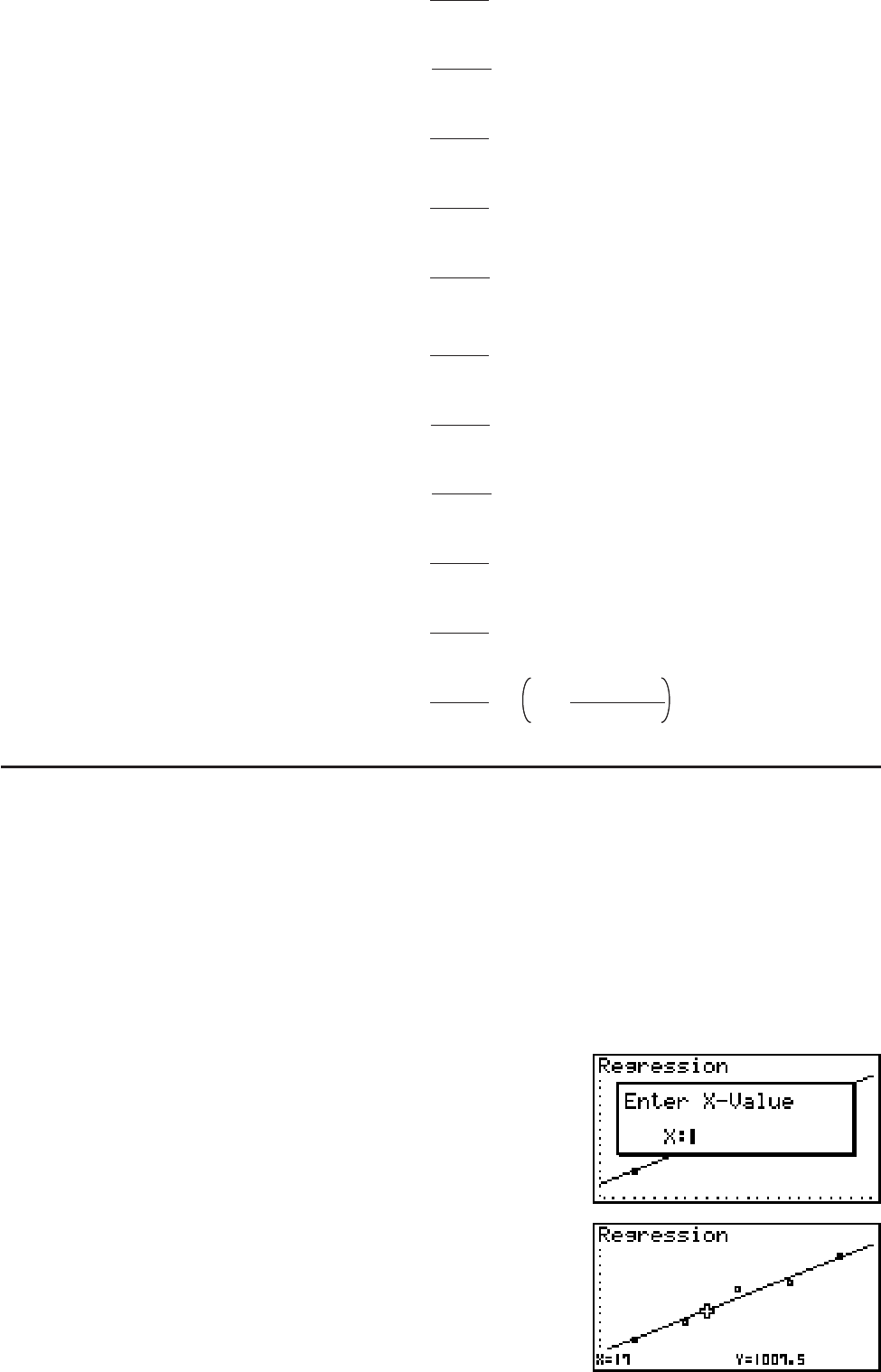
S Skønsmæssig værdiberegning for regressionsgrafer
Tilstanden STAT indeholder også en Y-CAL-funktion, der gør brug af regression til beregning af
den skønsmæssige y-værdi for en bestemt x-værdi efter at have tegnet en statistisk regression
med to variable.
Følgende er den almindelige procedure for brug af Y-CAL-funktionen.
1. Når du har tegnet en regressionsgraf, skal du trykke på (G-SLV)(Y-CAL) for at gå
ind i grafvalgstilstanden og derefter trykke på U.
Hvis der er flere grafer på skærmen, skal du bruge D og A til at vælge den ønskede graf,
og derefter trykke på U.
• Herefter vises en dialogboks til indtastning af en
x-værdi.
2. Indtast den ønskede værdi for
x og tryk derefter på U.
• Herefter vises koordinaterne for
x og y nederst på
skærmen, og markøren flyttes til det tilsvarende punkt
på grafen.
M
Se =
1
n – 2
i=1
n
(y
i
– (ax
i
+ b))
2
M
Se =
1
n – 2
i=1
n
(y
i
– (ax
i
+ b))
2
M
Se =
1
n – 2
i=1
n
(yi – (a + bxi))
2
M
Se =
1
n – 2
i=1
n
(yi – (a + bxi))
2
M
Se =
1
n – 3
i=1
n
(y
i
– (ax
i
+ bx
i
+ c))
2
2
M
Se =
1
n – 3
i=1
n
(y
i
– (ax
i
+ bx
i
+ c))
2
2
M
Se =
1
n – 4
i=1
n
(y
i
– (ax
i
3
+ bx
i
+ cx
i
+ d ))
2
2
M
Se =
1
n – 4
i=1
n
(y
i
– (ax
i
3
+ bx
i
+ cx
i
+ d ))
2
2
M
Se =
1
n – 5
i=1
n
(yi – (axi
4
+ bxi
3
+ cxi
+ dxi
+ e))
2
2
M
Se =
1
n – 5
i=1
n
(yi – (axi
4
+ bxi
3
+ cxi
+ dxi
+ e))
2
2
M
Se =
1
n – 2
i=1
n
(yi – (a + b ln xi ))
2
M
Se =
1
n – 2
i=1
n
(yi – (a + b ln xi ))
2
M
Se =
1
n – 2
i=1
n
(ln y
i
– (ln a + bx
i
))
2
M
Se =
1
n – 2
i=1
n
(ln y
i
– (ln a + bx
i
))
2
M
Se =
1
n – 2
i=1
n
(ln yi – (ln a + (ln b) · xi ))
2
M
Se =
1
n – 2
i=1
n
(ln yi – (ln a + (ln b) · xi ))
2
M
Se =
1
n – 2
i=1
n
(ln y
i
– (ln a + b ln x
i
))
2
M
Se =
1
n – 2
i=1
n
(ln y
i
– (ln a + b ln x
i
))
2
M
Se =
1
n – 2
i=1
n
(yi – (a sin (bxi + c) + d ))
2
M
Se =
1
n – 2
i=1
n
(yi – (a sin (bxi + c) + d ))
2
M
Se =
1
n – 2 1 + ae
–bx
i
C
i=1
n
y
i
–
2
M
Se =
1
n – 2 1 + ae
–bx
i
C
i=1
n
y
i
–
2










