User manual - fx-50F_PLUS
G-52
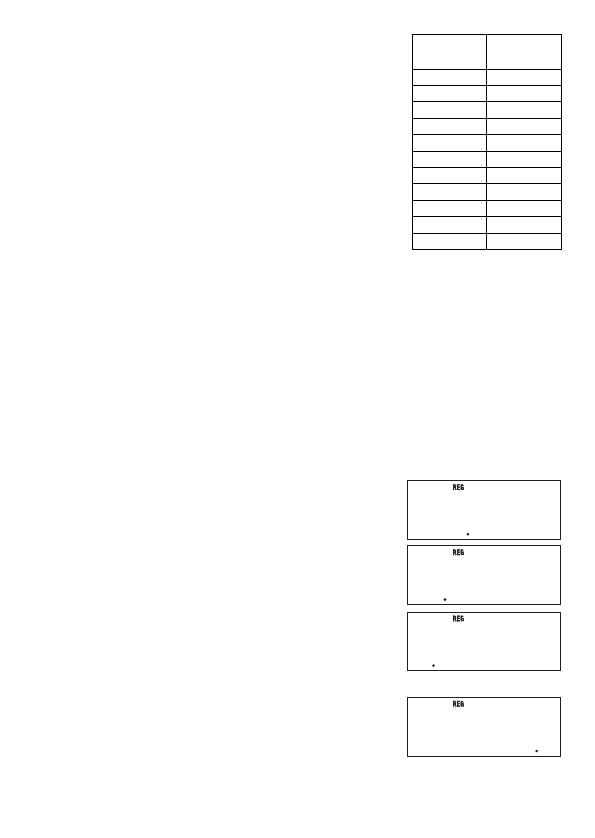
Beispiel 2: Die nebenstehenden Daten zeigen das Gewicht
eines Neugeborenen an verschiedenen Tagen
nach der Geburt.
1
Ermitteln Sie die Regressionsformel und den Korrelations-
koeffi zienten über die lineare Regression der Daten.
2
Ermitteln Sie die Regressionsformel und den Korrelations-
koeffi zienten über die logarithmische Regression der Daten.
3
Sagen Sie auf Basis der geeignetesten Regressionsformel
für den Datentrend gemäß den Regressionsergebnissen das
350 Tage nach der Geburt zu erwartende Gewicht voraus.
Bedienungsvorgang
REG-Modus aufrufen und lineare Regression wählen:
N
5
(REG)
1
(Lin)
FreqOff als Einstellung für statistische Häufi gkeit wählen:
1N
(SETUP)
dd
2
(FreqOff)
Probendaten eingeben:
20,3150
m
(DT)
50,4800
m
(DT)
80,6420
m
(DT)
110,7310
m
(DT)
140,7940
m
(DT)
170,8690
m
(DT)
200,8800
m
(DT)
230,9130
m
(DT)
260,9270
m
(DT)
290,9310
m
(DT)
320,9390
m
(DT)
1
Lineare Regression
Regressionsformel-Konstantenterm a:
1
2
(S-VAR)
1
(VAR)
ee
1
(a)
E
Regressionskoeffi zient b:
1
2
(S-VAR)
1
(VAR)
ee
2
(b)
E
Korrelationskoeffi zient:
1
2
(S-VAR)
1
(VAR)
ee
3
(
r
)
E
2
Logarithmische Regression
Logarithmische Regression wählen:
1
2
(S-VAR)
3
(TYPE)
2
(Log)
a
4446575758
a
4446575758
b
1887575758
b
1887575758
r
0904793561
r
0904793561
20
x
1
=
20
x
1
=
Zahl der
Tage
Gewicht
(g)
20 3150
50 4800
80 6420
110 7310
140 7940
170 8690
200 8800
230 9130
260 9270
290 9310
320 9390










