User Manual

Chapitre 16 : Application Calcul différentiel interactif 281
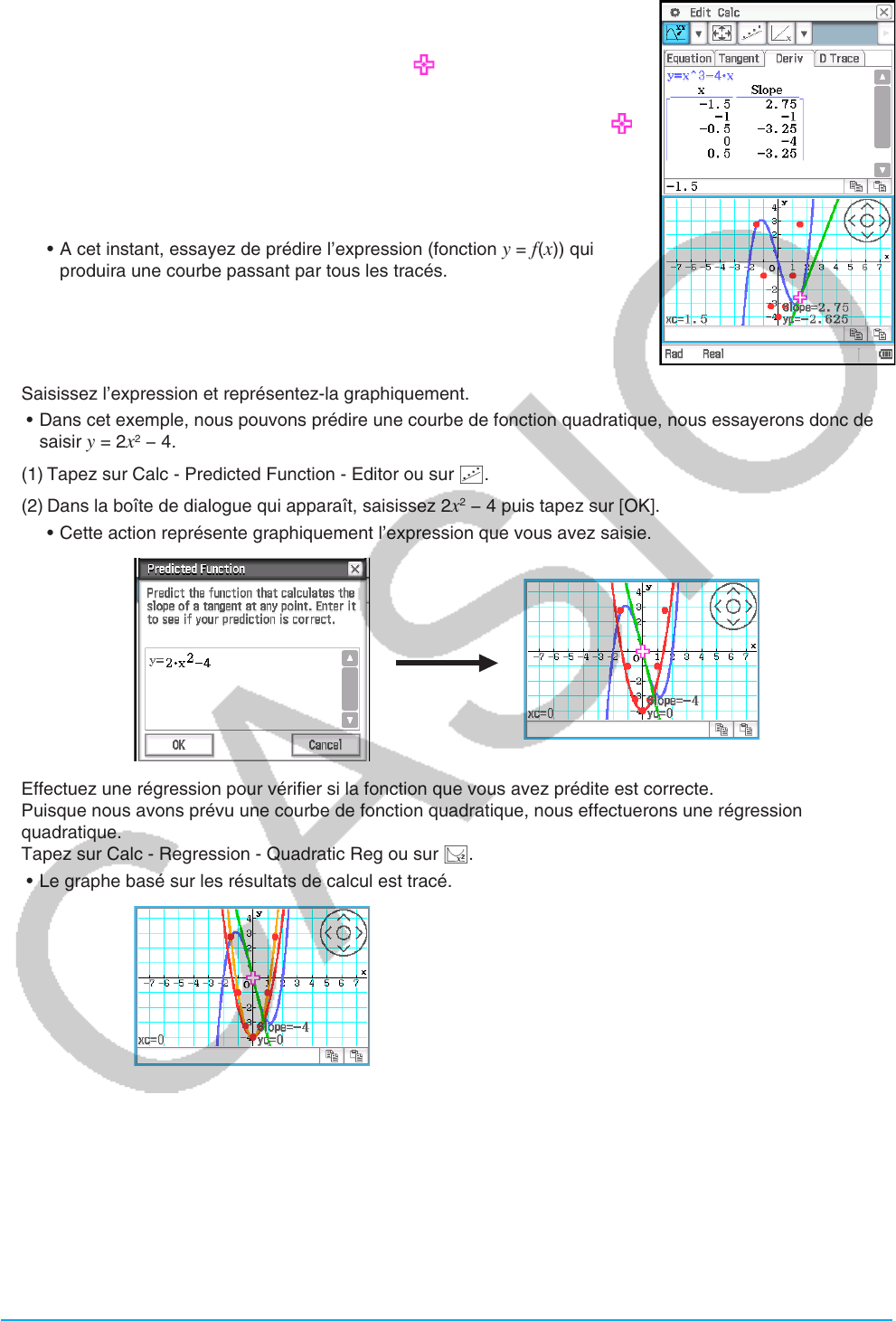
4. Dans la fenêtre graphique DiffCalc, tracez un point aux coordonnées (
x,
pente).
(1) Utilisez les boutons du curseur pour déplacer
autour du graphe.
(2) Tapez sur le bouton [EXE].
• Cela ajoutera les valeurs de
x et de la pente à la position actuelle de
sur la table numérique dans l’onglet [Deriv]. Au même moment, la (x,
pente) sera tracée sur la fenêtre graphique DiffCalc.
(3) Répétez les étapes (1) et (2) ci-dessus pour tracer au moins quatre
points.
• A cet instant, essayez de prédire l’expression (fonction
y = f (x)) qui
produira une courbe passant par tous les tracés.
5. Saisissez l’expression et représentez-la graphiquement.
• Dans cet exemple, nous pouvons prédire une courbe de fonction quadratique, nous essayerons donc de
saisir
y = 2x
2
− 4.
(1) Tapez sur Calc - Predicted Function - Editor ou sur D.
(2) Dans la boîte de dialogue qui apparaît, saisissez 2
x
2
− 4 puis tapez sur [OK].
• Cette action représente graphiquement l’expression que vous avez saisie.
6. Effectuez une régression pour vérifier si la fonction que vous avez prédite est correcte.
Puisque nous avons prévu une courbe de fonction quadratique, nous effectuerons une régression
quadratique.
Tapez sur Calc - Regression - Quadratic Reg ou sur f.
• Le graphe basé sur les résultats de calcul est tracé.
Conseil : Quatre types de régression sont disponibles dans le menu Calc - Regression. Choisissez le type de calcul de
régression que vous voulez effectuer selon les droites et les courbes prévues de la forme des tracés.
Remarque
• Dans l’étape 4 de la procédure ci-dessus, assurez-vous de tracer au moins quatre points pour les
coordonnées (x, pente). Tenter d’effectuer les étapes à partir de l’étape 5 lorsqu’il y a moins de quatre tracés
fait apparaitre le message « Plot at least 4 points. » qui vous informe que vous ne pouvez pas continuer avant
d’avoir tracé plus de points.