User Manual

Chapitre 16 : Application Calcul différentiel interactif 280
• Utilisez les touches du pavé directionnel pour déplacer le point D et pour observer la pente de la sécante
DE et Eq (équation) de la sécante DE juste avant et juste après la position où le point D et le point E sont
identiques. Cela vous permet d’étudier la pente de l’expression de la tangente
y = x
2
− 2.
Remarque
• Pour changer le point (D ou E) qui se déplace lorsque vous appuyez sur la touche gauche ou droite du
curseur, appuyez sur la touche haut ou bas du pavé directionnel, ou tapez sur 9 ou 8. Le point qui sera
déplacé lorsque vous appuierez sur la touche gauche ou droite du curseur est indiqué par
.
• Vous pouvez également déplacer le point E ou le point D avec le stylet. Tapez et maintenez enfoncés un des
points avec le stylet, puis faites-le glisser vers l’emplacement où vous souhaitez le déplacer.
16-2 Dérivation de la dérivée à l’aide de l’onglet [Deriv]
u Utiliser l’onglet [Deriv]
Exemple : La pente de la tangent en un point (x, y) sur le graphe de y = x
3
− 4x, est pente. Tracez les
coordonnées (x
1
, pente
1
), (x
2
, pente
2
), (x
3
, pente
3
), …. (x
n
, pente
n
) dans la fenêtre graphique DiffCalc, et
prédisez la fonction qui passe par tous les tracés. Utilisez également la régression pour confirmer la fonction.
1. Dans la fenêtre de la table DiffCalc, affichez l’onglet [Function].
2. A la ligne «
y: » sous « Function», saisissez x
3
− 4x.
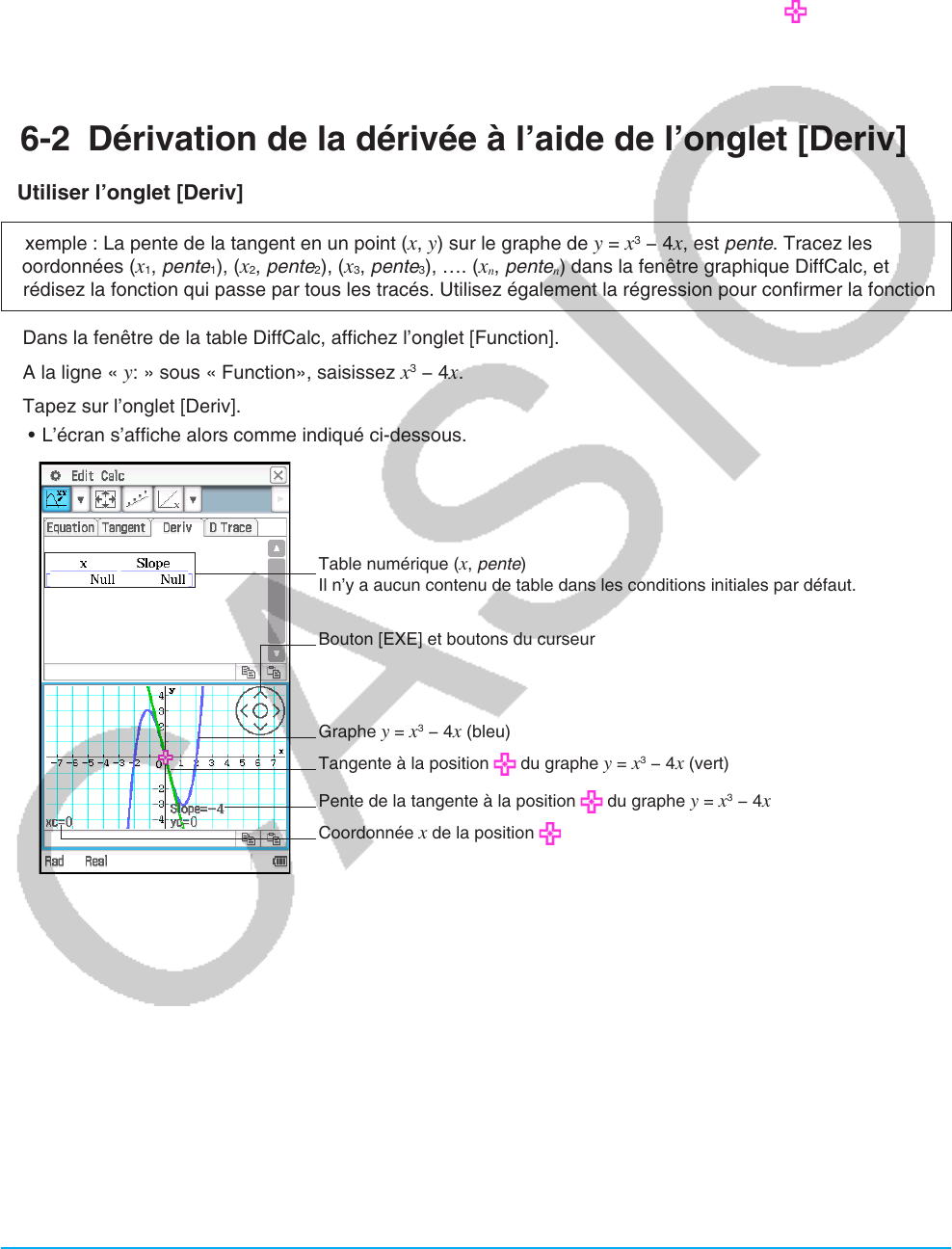
3. Tapez sur l’onglet [Deriv].
• L’écran s’affiche alors comme indiqué ci-dessous.
Table numérique (x, pente)
Il n’y a aucun contenu de table dans les conditions initiales par défaut.
Bouton [EXE] et boutons du curseur
Graphe
y = x
3
− 4x (bleu)
Tangente à la position
du graphe y = x
3
− 4x (vert)
Pente de la tangente à la position
du graphe y = x
3
− 4x
Coordonnée x de la position