User Manual
Table Of Contents
- Table des matières
- Chapitre 1 : Bases
- Chapitre 2 : Application Principale
- 2-1 Calculs de base
- 2-2 Emploi de l’historique des calculs
- 2-3 Calculs de fonctions
- 2-4 Calculs de listes
- 2-5 Calculs de matrices et de vecteurs
- 2-6 Spécification d’une base numérique
- 2-7 Emploi du menu Action
- 2-8 Emploi du menu Interactif
- 2-9 Emploi de l’application Principale en combinaison avec d’autres applications
- 2-10 Utilisation de la fonction Vérifier
- 2-11 Emploi de Probabilité
- 2-12 Exécution d’un programme dans l’application Principale
- Chapitre 3 : Application Graphe & Table
- Chapitre 4 : Application Coniques
- Chapitre 5 : Application Graphes d’équations différentielles
- 5-1 Représentation graphique d’une équation différentielle
- 5-2 Tracé de graphes d’une fonction de type f(x) et de graphes d’une fonction paramétrique
- 5-3 Visualisation des coordonnées d’un graphe
- 5-4 Représentation graphique d’une expression ou valeur en la déposant dans la fenêtre graphique d’équation différentielle
- Chapitre 6 : Application Suites
- Chapitre 7 : Application Statistiques
- Chapitre 8 : Application Géométrie
- Chapitre 9 : Application Résolution numérique
- Chapitre 10 : Application eActivity
- Chapitre 11 : Application Finances
- Chapitre 12 : Application Programme
- Chapitre 13 : Application Spreadsheet
- Chapitre 14 : Application Graphe 3D
- Chapitre 15 : Application Plot Image
- Chapitre 16 : Application Calcul différentiel interactif
- Chapitre 17 : Application Physium
- Chapitre 18 : Application Système
- Chapitre 19 : Communication de données
- Appendice
- Mode Examen
Chapitre 16 : Application Calcul différentiel interactif 279
Onglet [D Trace] uniquement
• Afficher la boîte de dialogue de saisie de table pour configurer le réglage du pas de la valeur x ..............8
• Échanger une table numérique parmi 3 combinaisons de type de valeur
(
x, y1, y2; x, y2, y3; x, y1, y2, y3) ...........................................................................................................;
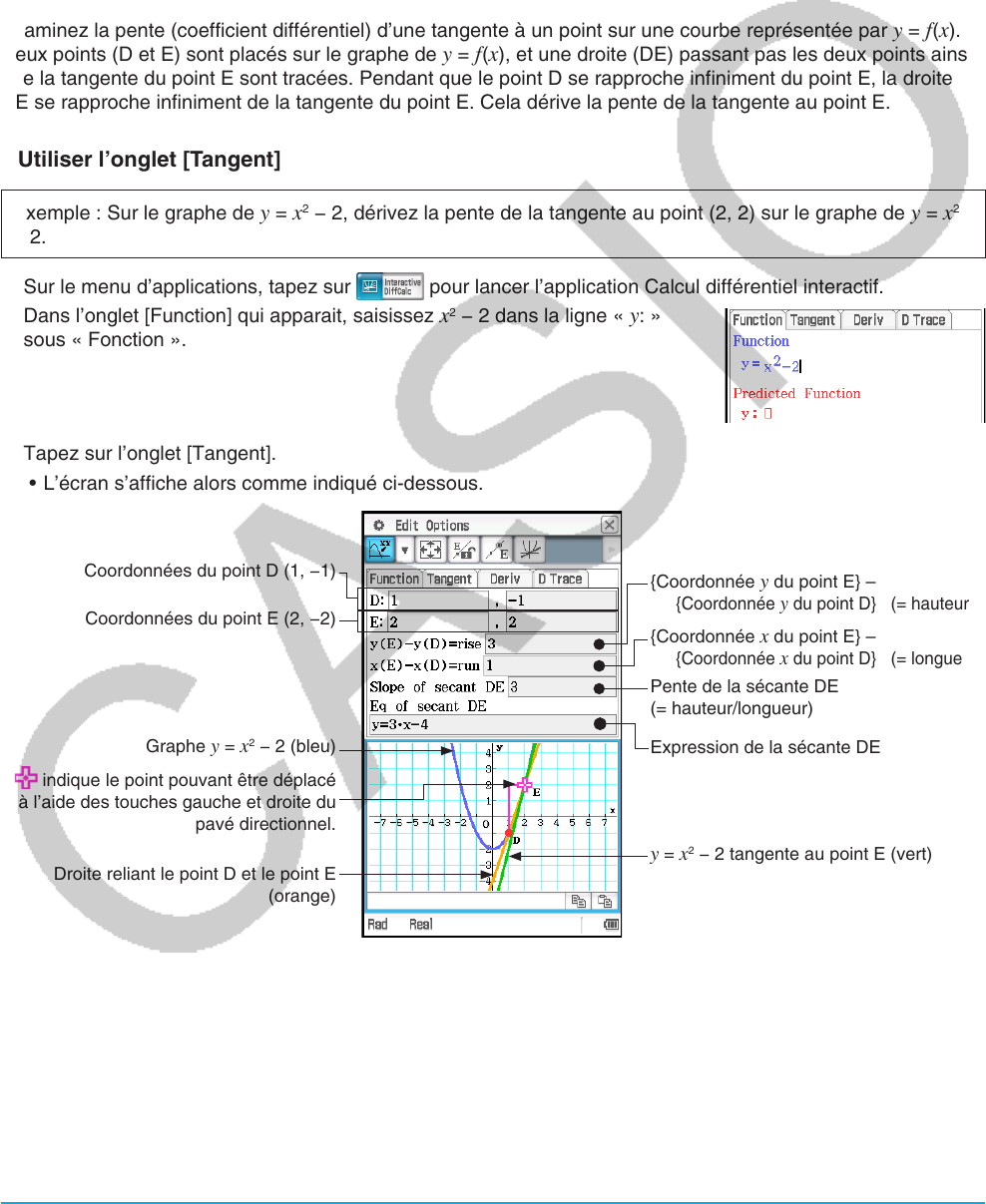
16-1 Connaitre les tangentes en utilisant l’onglet
[Tangent]
Examinez la pente (coefficient différentiel) d’une tangente à un point sur une courbe représentée par y = f (x).
Deux points (D et E) sont placés sur le graphe de y = f (x), et une droite (DE) passant pas les deux points ainsi
que la tangente du point E sont tracées. Pendant que le point D se rapproche infiniment du point E, la droite
DE se rapproche infiniment de la tangente du point E. Cela dérive la pente de la tangente au point E.
u Utiliser l’onglet [Tangent]
Exemple : Sur le graphe de y = x
2
− 2, dérivez la pente de la tangente au point (2, 2) sur le graphe de y = x
2
− 2.
1. Sur le menu d’applications, tapez sur
pour lancer l’application Calcul différentiel interactif.
2. Dans l’onglet [Function] qui apparait, saisissez
x
2
− 2 dans la ligne « y: »
sous « Fonction ».
3. Tapez sur l’onglet [Tangent].
• L’écran s’affiche alors comme indiqué ci-dessous.
Coordonnées du point D (1, −1)
Coordonnées du point E (2, −2)
Graphe
y = x
2
− 2 (bleu)
indique le point pouvant être déplacé
à l’aide des touches gauche et droite du
pavé directionnel.
Droite reliant le point D et le point E
(orange)
{Coordonnée y du point E} –
{Coordonnée y du point D} (= hauteur)
{Coordonnée x du point E} –
{Coordonnée x du point D} (= longueur)
Pente de la sécante DE
(= hauteur/longueur)
Expression de la sécante DE
y = x
2
− 2 tangente au point E (vert)
4. Tapez sur w (ou Point - Fix Point E).
• Cela verrouille le point E et permet de repositionner le point D uniquement.
5. Utilisez les touches gauche et droite du pavé directionnel pour rapprocher le point D du point E sur le graphe
y = x
2
− 2.
6. Déplace le point D au même endroit que le point E.
• Hauteur et longueur dans l’onglet [Tangent] prennent la valeur 0, et seule la tangente
y = x
2
− 2 (vert) du
point E (similaire au point D) demeure affichée.










