User Manual
Table Of Contents
- Table des matières
- Chapitre 1 : Bases
- Chapitre 2 : Application Principale
- 2-1 Calculs de base
- 2-2 Emploi de l’historique des calculs
- 2-3 Calculs de fonctions
- 2-4 Calculs de listes
- 2-5 Calculs de matrices et de vecteurs
- 2-6 Spécification d’une base numérique
- 2-7 Emploi du menu Action
- 2-8 Emploi du menu Interactif
- 2-9 Emploi de l’application Principale en combinaison avec d’autres applications
- 2-10 Utilisation de la fonction Vérifier
- 2-11 Emploi de Probabilité
- 2-12 Exécution d’un programme dans l’application Principale
- Chapitre 3 : Application Graphe & Table
- Chapitre 4 : Application Coniques
- Chapitre 5 : Application Graphes d’équations différentielles
- 5-1 Représentation graphique d’une équation différentielle
- 5-2 Tracé de graphes d’une fonction de type f(x) et de graphes d’une fonction paramétrique
- 5-3 Visualisation des coordonnées d’un graphe
- 5-4 Représentation graphique d’une expression ou valeur en la déposant dans la fenêtre graphique d’équation différentielle
- Chapitre 6 : Application Suites
- Chapitre 7 : Application Statistiques
- Chapitre 8 : Application Géométrie
- Chapitre 9 : Application Résolution numérique
- Chapitre 10 : Application eActivity
- Chapitre 11 : Application Finances
- Chapitre 12 : Application Programme
- Chapitre 13 : Application Spreadsheet
- Chapitre 14 : Application Graphe 3D
- Chapitre 15 : Application Plot Image
- Chapitre 16 : Application Calcul différentiel interactif
- Chapitre 17 : Application Physium
- Chapitre 18 : Application Système
- Chapitre 19 : Communication de données
- Appendice
- Mode Examen
Chapitre 11: Application Finances 197
u Lors du calcul de I%
i
(taux d’intérêt effectif) est calculé avec la méthode de Newton.
× PV + × PMT + × FV = 0
I% est calculé à partir de i en utilisant les formules ci-dessous :
Lorsque P/Y = C/Y = 1 Lorsque P/Y 1 et/ou C/Y 1
I% =
Les calculs de l’intérêt (
I%) s’effectuent selon la méthode de Newton, qui produit des valeurs approximatives
dont la précision peut être affectée par divers facteurs. Il est nécessaire de tenir compte de ce fait lors du calcul
d’intérêts, ou bien de vérifier d’une autre façon les résultats.
Marge brute d’autofinancement
NPV = CF0 + + + + … +
(1+ i)
CF
1
(1+ i)
2
CF2
(1+ i)
3
CF3
(1+ i)
n
CFn
(
=
100
%
,
n : entier naturel jusqu’à 80)
NFV = NPV × (1 + i )
n
IRR est calculé selon la méthode de Newton.
0 = CF
0 + + + + … +
(1+ i)
CF
1
(1+ i)
2
CF2
(1+ i)
3
CF3
(1+ i)
n
CFn
Dans cette formule, NPV = 0, et la valeur de IRR équivalent à i × 100. Il faut toutefois noter que des valeurs
fractionnaires minimes tendent à s’accumuler au cours des calculs effectués ensuite par le ClassPad et que le
NPV n’atteint jamais exactement zéro. Plus NPV s’approche de zéro, plus IRR est précis.
PBP =
{
0 .................................. (CF0 t 0)
n –
NPV
n
NPVn+1 – NPVn
(Autre que ci-dessus)
...
NPVn =
Σ
n
k
= 0
CFk
(1 + i)
k
n : l’entier positif le plus petit remplissant les conditions
NPVn s 0, 0 s NPVn+1, ou 0
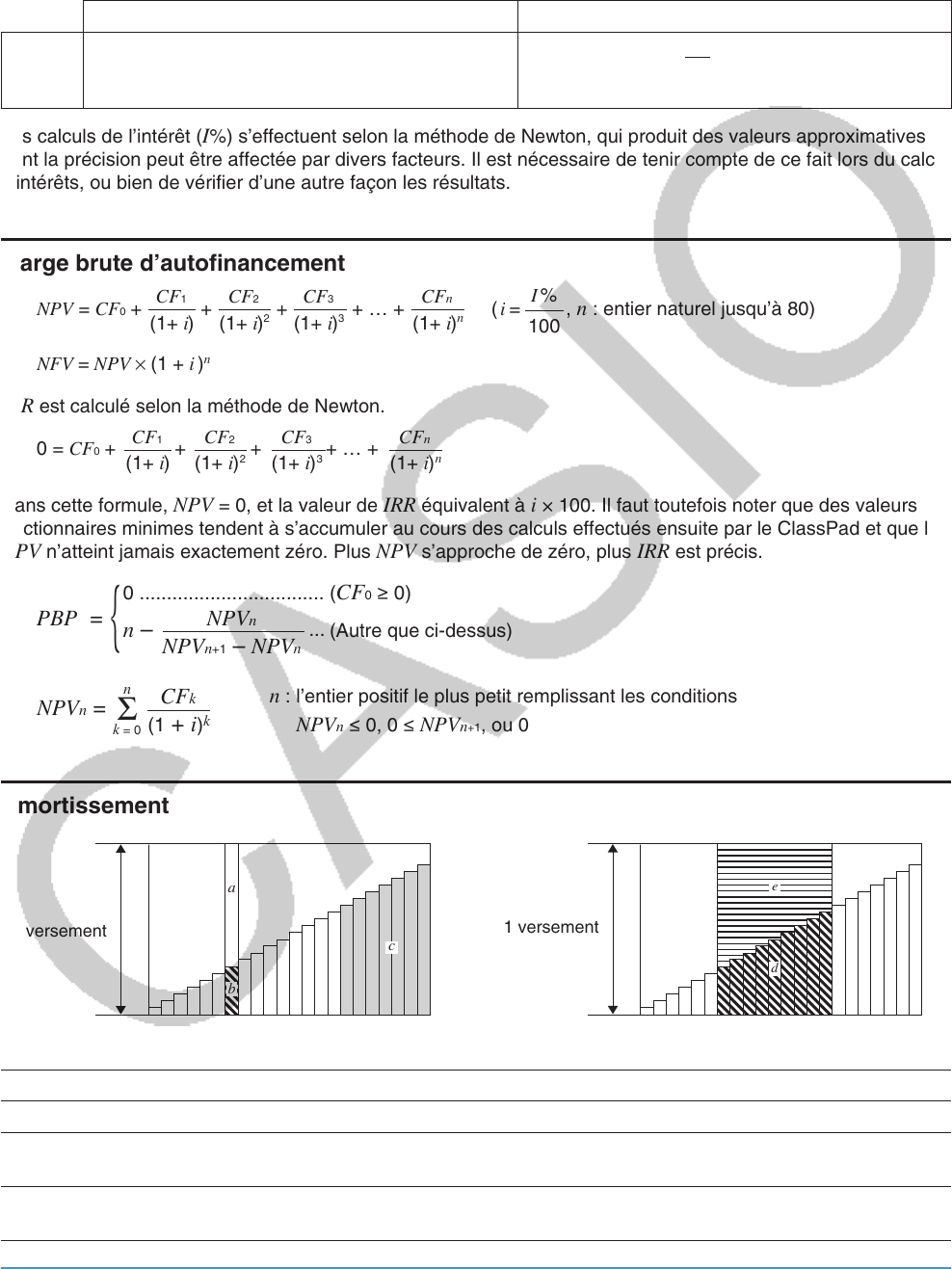
Amortissement
c
a
1 versement
Nombre de versements
1 PM1 PM2 Dernier............ ................... ........
b
1 versement
Nombre de versements
1 PM1
PM2
Dernier............. ................
...........
e
d
a : part de l’intérêt du versement PM1 (INT)
b : part du capital du versement PM1 (PRN)
c : capital restant dû après versement PM2
(BAL)
d : capital total payé du versement PM1 au
versement PM2 (ΣPRN)
i × 100
( )
×
C/Y
×
100
(1 + i )–1
P/Y
C/Y
PM1=I PM1–1 ×I × ( )
PM1=+PM1–1 ×
PM2=PM2–1 +PM2
Σ
=PM1 +PM1+1 + … + PM2
PM2
PM1










