User manual - File 3

u 378 u
x
y
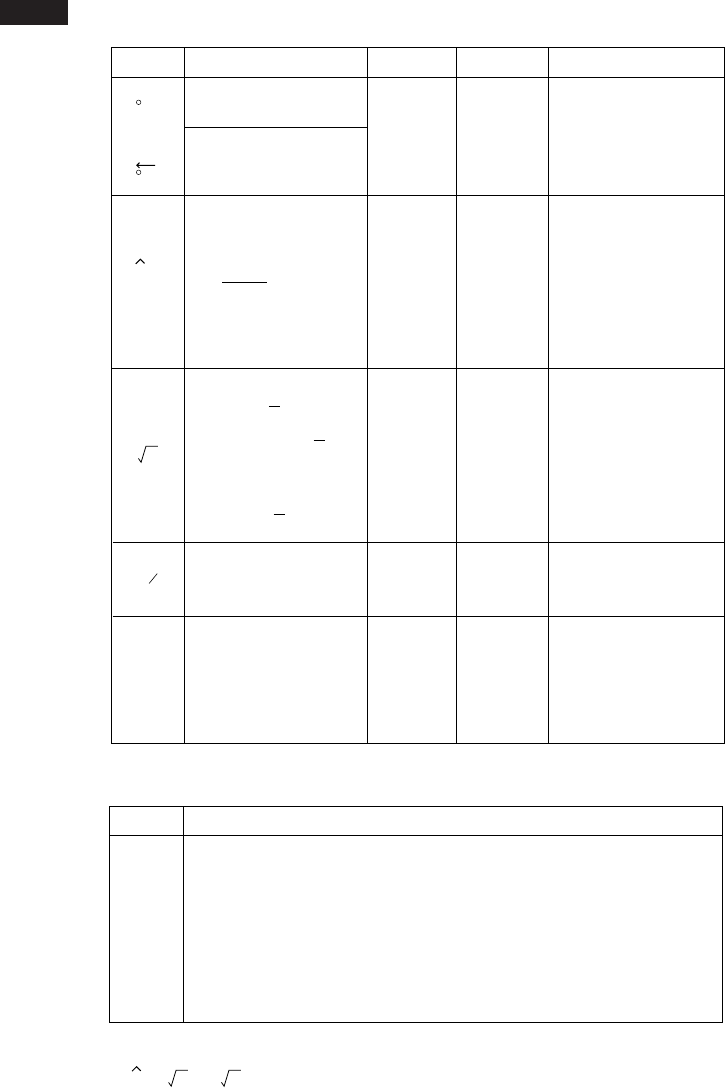
関数 入 力 範 囲 内部演算桁数 精 度
備 考
〃 〃
〃 〃
〃 〃
〃 〃
’ ”
’ ”
│a│, b, c＜１×１０
１００
０≦b, c
│x│＜１×１０
１００
６０ 進表示は
│x│＜１×１０
７
x＞０：
−１×１０
１００
＜y log x＜１００
x＝０： y＞０
x＜０：
(x
y
)
y＝n, (n は整数
または分数)
ただし、
−１×１０
１００
＜ log│x│
＜１００
２n＋１
１
1
１
y
y＞０： x ０
−１×１０
１００
＜ log y＜１００
y ＝０： x＞０
x
1
x
y＜０： x＝２n＋１,
n
n G０, ( n は整数
または 分数)
ただし、
−１×１０
１００
＜ log│y│
＜１００
整数・分子・分母の合計が
１０桁以内 (ただし、区切り
シンボルを含む)。
a
b
c
≠
原則として
１０桁目±１
※
１５桁
STAT
│x│＜１×１０
５０
│y│＜１×１０
５０
│n│＜１×１０
１００
xσn , yσn , o , p
a, b , c , d , e , r：n ０
xσ
n−1, yσn−1：n ０, １
≠
≠
関数
入 力 範 囲
(x
y
)
x
y
n進計算
変換後の値が次の範囲
Dec：−２１４７４８３６４８≦x≦２１４７４８３６４７
Bin ：１０００００００００００００００ ≦x≦1111111111111111(負)
０≦x≦０111111111111111 (０, 正)
Oct：２００００００００００≦ x≦３７７７７７７７７７７ (負)
０≦x≦１７７７７７７７７７７(０, 正)
Hex ：８０００００００≦ x≦FFFFFFFF(負)
０≦x≦７FFFFFFF(０, 正)
※ 一回での計算誤差は10桁目±1の誤差となります。(指数で表示する場合には誤差は表示している
仮数表示の最下位桁±1となります。)ただし連続計算を行なった場合には、誤差が累積されます。
( , , x ! ,
３
, n Pr , nCr , 等内部で連続演算を行なう場合も、同様に誤差が累積されます。)
また、関数の特異点や変曲点の近傍で、誤差が累積されて大きくなることがあります。
4
関数の入力範囲と精度
GY-355/357/359巻末.J-m0312n 04.11.18, 14:11378